The ESPRIT Algorithm and Central Limit Error Scaling

The ESPRIT algorithm starts by rearranging the noisy measurements into a Hankel or Toeplitz matrix. In this paper, we consider the Toeplitz version


This content originally appeared on HackerNoon and was authored by Algorithmic Bias (dot tech)

Abstract and 1 Introduction

1.1 ESPRIT algorithm and central limit error scaling

1.2 Contribution

1.3 Related work

1.4 Technical overview and 1.5 Organization

2 Proof of the central limit error scaling

3 Proof of the optimal error scaling

4 Second-order eigenvector perturbation theory

5 Strong eigenvector comparison

5.1 Construction of the “good” P

5.2 Taylor expansion with respect to the error terms

5.3 Error cancellation in the Taylor expansion

5.4 Proof of Theorem 5.1

A Preliminaries

B Vandermonde matrice

C Deferred proofs for Section 2

D Deferred proofs for Section 4

E Deferred proofs for Section 5

F Lower bound for spectral estimation

References

1.1 ESPRIT algorithm and central limit error scaling

\

\ Define the location and intensity vectors

\

\ The minimum is taken over all permutations π on {1, . . . , r}.

\

\

\

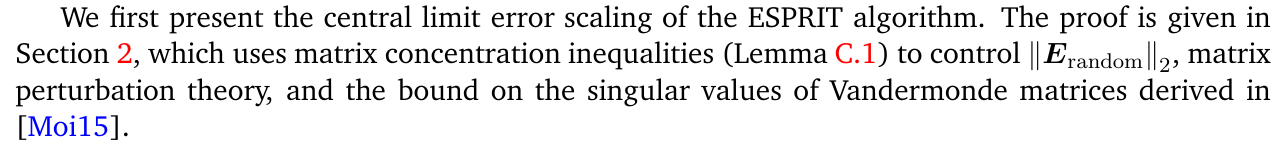
:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\


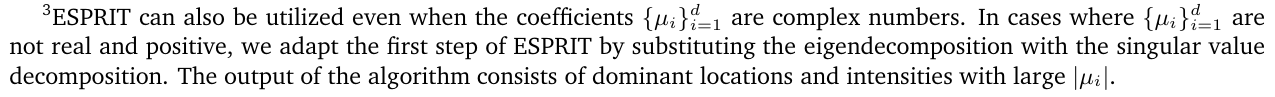
This content originally appeared on HackerNoon and was authored by Algorithmic Bias (dot tech)


Print Share Comment Cite Upload Translate Updates
APA

Algorithmic Bias (dot tech) | Sciencx (2025-05-08T16:00:25+00:00) The ESPRIT Algorithm and Central Limit Error Scaling. Retrieved from https://www.scien.cx/2025/05/08/the-esprit-algorithm-and-central-limit-error-scaling/

MLA
" » The ESPRIT Algorithm and Central Limit Error Scaling." Algorithmic Bias (dot tech) | Sciencx - Thursday May 8, 2025, https://www.scien.cx/2025/05/08/the-esprit-algorithm-and-central-limit-error-scaling/
HARVARD
Algorithmic Bias (dot tech) | Sciencx Thursday May 8, 2025 » The ESPRIT Algorithm and Central Limit Error Scaling., viewed ,<https://www.scien.cx/2025/05/08/the-esprit-algorithm-and-central-limit-error-scaling/>
VANCOUVER
Algorithmic Bias (dot tech) | Sciencx - » The ESPRIT Algorithm and Central Limit Error Scaling. [Internet]. [Accessed ]. Available from: https://www.scien.cx/2025/05/08/the-esprit-algorithm-and-central-limit-error-scaling/
CHICAGO
" » The ESPRIT Algorithm and Central Limit Error Scaling." Algorithmic Bias (dot tech) | Sciencx - Accessed . https://www.scien.cx/2025/05/08/the-esprit-algorithm-and-central-limit-error-scaling/
IEEE
" » The ESPRIT Algorithm and Central Limit Error Scaling." Algorithmic Bias (dot tech) | Sciencx [Online]. Available: https://www.scien.cx/2025/05/08/the-esprit-algorithm-and-central-limit-error-scaling/. [Accessed: ]
rf:citation
» The ESPRIT Algorithm and Central Limit Error Scaling | Algorithmic Bias (dot tech) | Sciencx | https://www.scien.cx/2025/05/08/the-esprit-algorithm-and-central-limit-error-scaling/ |

Please log in to upload a file.



There are no updates yet.
Click the Upload button above to add an update.

You must be logged in to translate posts. Please log in or register.

Related Posts