This content originally appeared on DEV Community and was authored by davyie
Introduction
Group allocation is a major part of organising students and teams in general. Therefore, it is a good idea to have a strategy for creating an allocation. We can achieve an allocation with multiple different methods e.g. random allocation or let the students choose their group etc. There are infinite number of methods to create group allocation but today we are going to take a look at a method that takes advantage of computer science theory, mainly the NP-Complete problem called Clique Problem!
Clique Problem
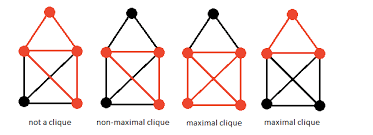
To understand Clique Problem we have to understand graphs. A graph consists of nodes and edges. A sub-graph is a subset of nodes with the same edges from the original graph. A complete graph is when all the nodes have edges with each other.
So one might ask themselves, what is the Clique Problem? It is one of the 21 NP-complete problems presented by Karp! This problem is a well studied problem by computer scientists and mathematicians that can be formulated in multiple ways. We can focus on the fourth definition on its Wikipedia page. We are gonna formulate the problem as the following
- Given a graph and a size, can we guarantee that the graph contains a complete sub-graph with a given size?
The size and graph can vary from different problem instances and currently we do not have an efficient algorithm to solve all the problem instances of the Clique problem. However, we have a bruteforce algorithm that works on small graphs such as the one we generated for Software Development academy. So, the next question is, how did we create the graph?
Creation of graph
To gather data about the graph we asked the students to answer two questions,
- Name one or two student(s) you feel is more knowledgeable in programming than you.
- Name one and two student(s) you trust and would give your phone to.
This allowed us to observe the connections between students in from three perspectives,
- Both questions
- First question
- Second question
Unfortunately I will not reveal what or which question(s) we used to create our graph.
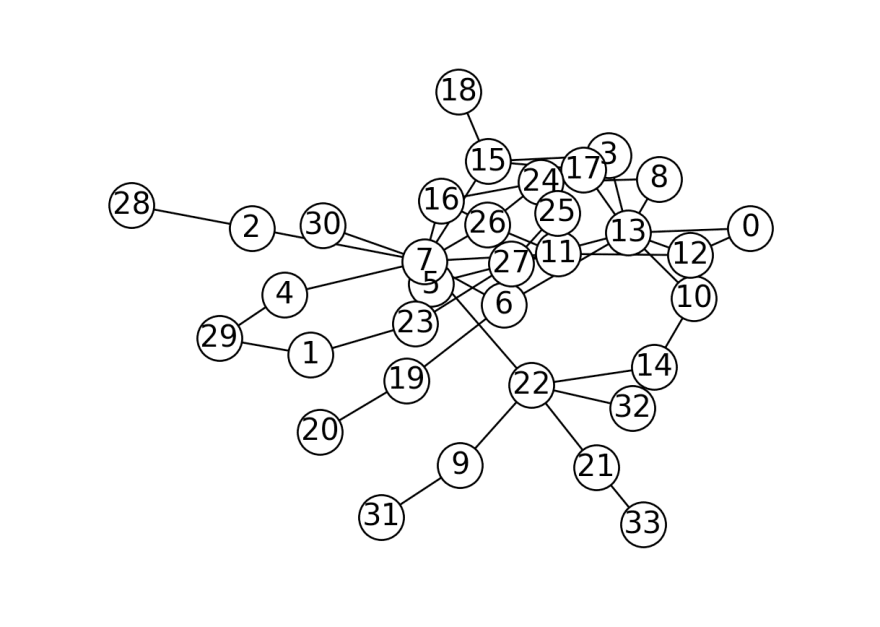Figure 1: All the nodes that had edges between them.
Now that we have our graph we can apply our algorithm on it!
Bruteforce algorithm
So the idea behind the bruteforce algorithm is to check a node's neighbours and their neighbours. If we come back from the starting node from all of its neighbours then we know that a clique exists. This algorithm does not work for all graphs but we can use it for a small instance, and in our case it is group allocation.
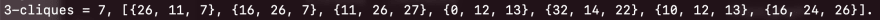Figure 2: The set of cliques the algorithm had found.
Once the algorithm has run we get a set of nodes that creates a clique. We can see that our algorithm generated some groups that share the same node(s). Thus, we cannot directly choose all set of groups but a subset groups for the final group allocation.
Issues
There are many issues with this approach and one of them is the missing responses for the two questions. Those nodes are stand alone but have to be integrated some how. We turn to randomisation! The nodes are randomly picked in which clique they are put in. We can add them in two ways, either direct or indirect to one of the nodes in the clique.
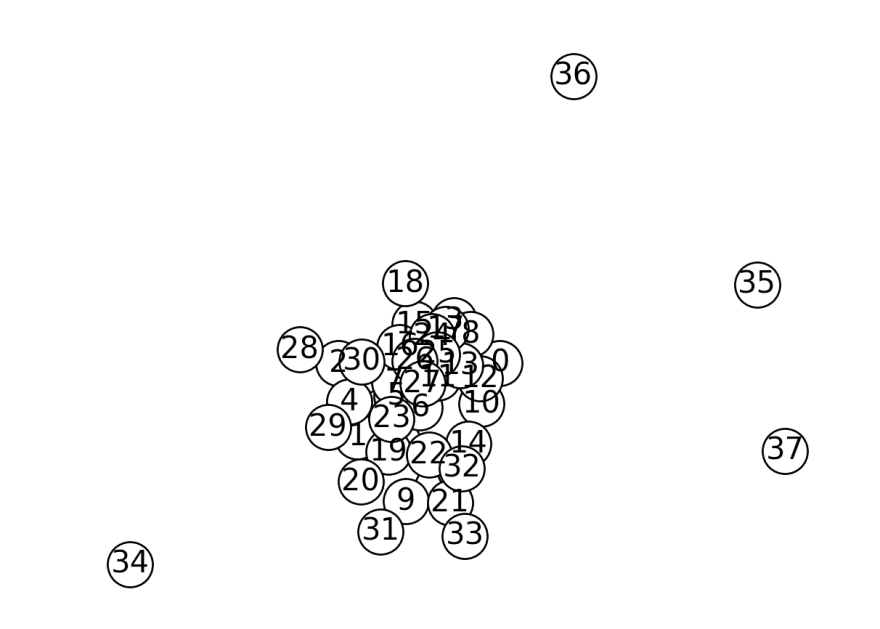Figure 3: All of the nodes in the graph
Second problem that occurred is the event of nodes connected to the graph was not included in the set of chosen cliques. Those have to be allocated as well! We then try to find an edge from that node to one of the cliques so it will have some connection to the group. And thus conclude our group allocation process for Backend Module!
Summary
We have gone through a short explanation of how the group allocation was made in the Backend Module in Software Engineering Academy. This is a compiled list of the steps,
- Send out a questionnaire to students to answer
- Create a graph based on the questionnaire
- Find the Cliques in the graph with bruteforce algorithm
- Choose a subset of the available Cliques
- Allocate nodes with some connection to a clique
- Allocate stand-alone nodes to each clique And now we are done with our group allocation! Hope this was fun to read and happy with your groups and how the groups was created for Backend Module!
Happy coding in Backend Module!
This content originally appeared on DEV Community and was authored by davyie
davyie | Sciencx (2021-04-06T20:27:53+00:00) Applying ideas from CS to solve group allocation. Retrieved from https://www.scien.cx/2021/04/06/applying-ideas-from-cs-to-solve-group-allocation/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.