This content originally appeared on DEV Community and was authored by Anne Quinkenstein
Graph
•Graph G(V, E) - Graph, welcher aus der Knoten- und Kantenmenge V und E besteht.
•Knoten v - Element aus V, der Menge der Knoten (v ∈ V)
•Kante e - Element aus E, der Menge der Kanten (e ∈ E)
ungerichteter Graph
E ⊆ { {i,j} : i ∈ V, j ∈ V, i ≠ j }
gerichteter Graph
E ⊆ { (i,j) : i ∈ V, j ∈ V }
Nachbarschaft
G = (V, E): gerichteter Graph.
•Zwei Knoten i, j ∈ V heißen benachbart, wenn eine Kante
zwischen ihnen verläuft, also (i, j) ∈ E oder (j, i) ∈ E.
•Schleife : Eine Kante (i, i) mit identischem Ausgangs- und Endknoten
Grad
GradG(v) = |{e(i, j) ∈ E : v = i ∨ v = j}|
Da jede Kante genau zwei Knoten verbindet ist die Summe aller
Knotengrade = 2∗|E|(Anzahl der Kanten)
Eingangsgrad
GradIN(v) = |{e(i, j) ∈ V : v = j}|
Ausgangsgrad
GradOUT(v) = |{e(i, j) ∈ V : v = i}|
Darstellung
Abstrakt
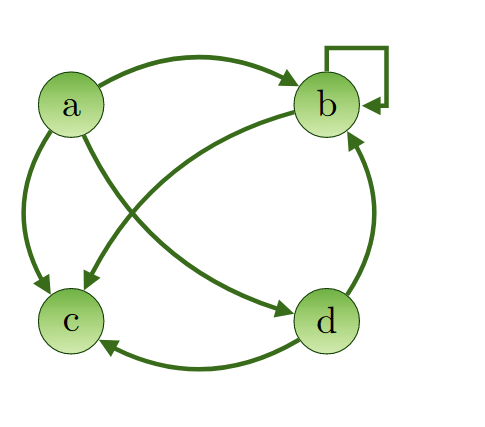
Sei G1(V1, E1)
•V1 = {a, b, c, d}
•E1 = { (a,b), (a,c), (a,d), (b,b), (b,c), (d,b), (d,c) }
graphisch
Adjazenzliste
Adjazenzmatrix
Weg
Weg in G ist ein Tupel (v0, v1, ..., vk), so dass für alle i mit 0 ≤ i < k gilt:
•(vi, vi+1) ∈ E für gerichtete Graphen
•{vi, vi+1} ∈ E für ungerichtete Graphen
•Das Tupel (v0, v1, ..., vk) wird dann ein Weg von v0 nach vk
genannt. k ist die Länge des Weges. k gibt also an, wie viele Kanten auf dem Weg durchlaufen werden.
einfach
kein Knoten kommt mehr als einmal in dem Weg vor
Kreis heißt einfach, wenn keine Kante mehrfach durchlaufen wird und ( abgesehen von Start- und Endknoten ) kein Knoten mehr als einmal in dem Weg vorkommt
azyklisch
Ein Graph heißt azyklisch, falls er keinen einfachen Kreis enthält.
zusammenhängend
ungerichteter Graph
G ist zusammenhängend, wenn für alle Knoten v, w ∈ V gilt: Es
gibt einen Weg von v nach w.
stark zusammenhängend
gerichteter Graph
G ist stark zusammenhängend, wenn für alle Knoten v, w ∈ V gilt: Es gibt einen Weg von v nach w.
Hamilton
Weg
Ein Weg W = (v0, ..., vk) ist ein Hamilton-Weg wenn jeder Knoten aus V genau einmal in W vorkommt
Kreis
Ein Weg W = (v0, ..., vk) ist ein Hamilton-Kreis wenn k > 1 und v0 = vk und (v0, ..., vk-1) ein Hamilton-Weg ist
Euler
ungerichteter Graph
Weg
Ein Weg W = (v0, ..., vk) ist ein Euler-Weg wenn W jede Kante aus E genau einmal durchläuft. D.h. für jedes e ∈ E genau ein
i ∈ {0, ..., k−1} gibt, so dass e = {vi, vi+1}
Kreis
Ein Weg W = (v0, ..., vk) ist ein Euler-Kreis wenn W ein Euler-Weg ist und v0 = vk.
isomorph
Zwei Graphen G1= (V1, E1) und G2= (V2, E2) heißen isomorph, wenn sie sich höchstens in der Bezeichnung ihrer Knoten
unterscheiden, ansonsten aber die selbe Struktur haben.
bijektive Funktion
f: V1⟶V2 existieren, mit den Eigenschaften:
•falls G1 und G2 gerichtete Graphen sind:
(u, v) ∈ E1 ⟷ (f(u), f(v)) ∈ E2
•falls G1 und G2 ungerichtete Graphen sind:
{u, v} ∈ E1 ⟷ {f(u), f(v)} ∈ E2
planar
wenn sich in der graphischen Darstellung keine zwei Kanten überkreuzen

gewichtet
eine Funktion, welche jeder Kante in G eine reelle Zahl (das Gewicht) zuordnet.
d: E ⟶ ℝ
Bäume
ungerichteter Baum B
B ist ein ungerichteter, zusammenhängender Graph G = (V, E), der keinen einfachen Kreis enthält.
Es existiert genau ein einfacher Weg, der die Knoten x und y
verbindet.
Spannbäume
This content originally appeared on DEV Community and was authored by Anne Quinkenstein
Anne Quinkenstein | Sciencx (2021-11-26T11:14:58+00:00) Graphen Cheat Sheet. Retrieved from https://www.scien.cx/2021/11/26/graphen-cheat-sheet/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.