This content originally appeared on HackerNoon and was authored by Anchoring
:::info Authors:
(1) Jongmin Lee, Department of Mathematical Science, Seoul National University;
(2) Ernest K. Ryu, Department of Mathematical Science, Seoul National University and Interdisciplinary Program in Artificial Intelligence, Seoul National University.
:::
1.1 Notations and preliminaries
2.1 Accelerated rate for Bellman consistency operator
2.2 Accelerated rate for Bellman optimality opera
5 Approximate Anchored Value Iteration
6 Gauss–Seidel Anchored Value Iteration
7 Conclusion, Acknowledgments and Disclosure of Funding and References
B Omitted proofs in Section 2
First, we prove the following lemma by induction.
\

\

\

\

\

\

\

\

\ Now, we present our key lemmas for the first rate of Theorem 2.
\

\
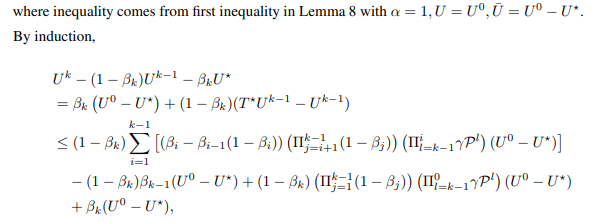
\ and let U¯ be the entire right hand side of inequality. Then, we have
\

\ By induction,
\
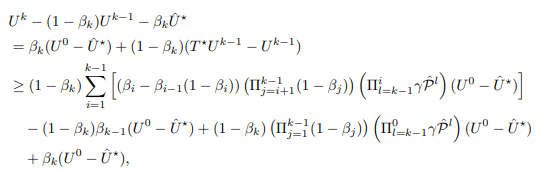
\ and let U¯ be the entire right hand side of inequality. Then, we have
\
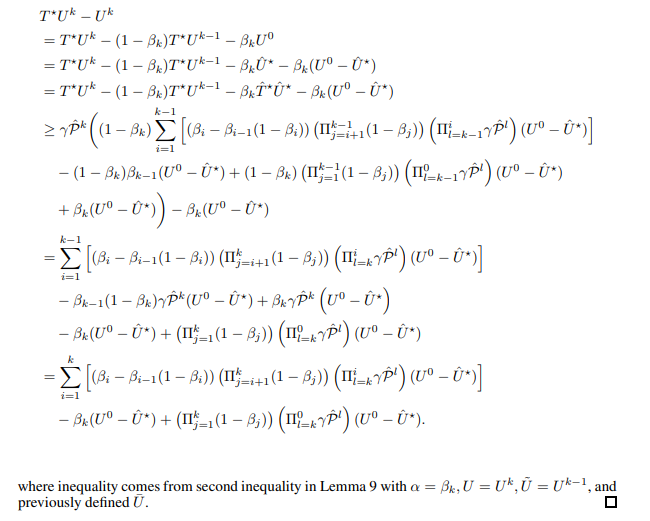
\ Now, we prove the first rate of Theorem 2.
\

\

\ where the second inequality is from the condition.
\ By induction,
\
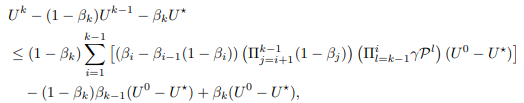
\ and let U¯ be the entire right hand side of inequality. Then, we have
\

\ Now, we prove the second rates of Theorem 2.
\

\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by Anchoring
Anchoring | Sciencx (2025-01-15T22:00:03+00:00) Breaking Down the Inductive Proofs Behind Faster Value Iteration in RL. Retrieved from https://www.scien.cx/2025/01/15/breaking-down-the-inductive-proofs-behind-faster-value-iteration-in-rl/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
