This content originally appeared on HackerNoon and was authored by Computational Technology for All
Table of Links
4 Members of Deep Π0 1 classes
6. Variants of Strong Depth

\ Proof. Suppose that X is not weakly deep. Then there is some computable measure µ such that X is µ-Martin-Lof random. By the Levin-Schnorr theorem for a priori complexity with respect to the measure µ (implicit in [Lev73]), there is some c such that
\ KA(X↾n) ≥ − log µ(X↾n) − c
\ for all n ∈ ω. Equivalently, we have
\
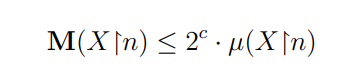
\ Since every computable measure is a computable semimeasure, the conclusion follows.
\ For the other direction, suppose that there is some computable, continuous semimeasure and some c ∈ ω such that for all n ∈ ω,
\

\ It thus follows from the Levin-Schnorr theorem for a priori complexity that X is µ-Martin-Lof random and hence is not weakly deep.
\ We define a sequence to be KA-deep if
\

\ (see the proof of [BDM23, Lemma 2.6] for discrete semimeasures which directly translates to the case of continuous semimeasures). Thus we can conclude:
\
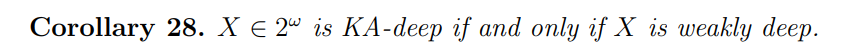
\ 6.2. Depth and monotone complexity. We can obtain a similar characterization of weak depth in terms of monotone complexity. Define a sequence to be Km-deep if
\
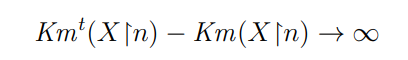
\ This notion was studied by Schnorr and Fuchs [SF77], who used the term super-learnable to refer to the failure of being Km-deep. In particular, Schnorr and Fuchs proved that a sequence is super-learnable if and only if it is Martin-Lof random with respect to a computable measure. Given that a sequence is weakly deep if and only if it is not Martin-Lof random with respect to a computable measure, we have the following.
\
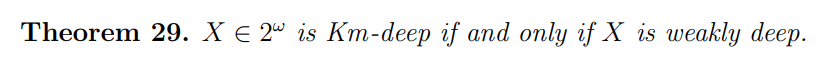
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
:::info Authors:
(1) Laurent Bienvenu;
(2) Christopher P. Porter.
:::
\
This content originally appeared on HackerNoon and was authored by Computational Technology for All
Computational Technology for All | Sciencx (2025-01-17T03:11:22+00:00) Bridging Computational Notions of Depth: Variants of Strong Depth. Retrieved from https://www.scien.cx/2025/01/17/bridging-computational-notions-of-depth-variants-of-strong-depth/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
