This content originally appeared on HackerNoon and was authored by Phenomenology Technology
Table of Links
2 Dark matter through ALP portal and 2.1 Introduction
2.3 Existing constraints on ALP parameter space
3 A two component dark matter model in a generic 𝑈(1)𝑋 extension of SM and 3.1 Introduction
3.3 Theoretical and experimental constraints
3.4 Phenomenology of dark matter
3.5 Relic density dependence on 𝑈(1)𝑋 charge 𝑥𝐻
4 A pseudo-scalar dark matter case in 𝑈(1)𝑋 extension of SM and 4.1 Introduction
4.3 Theoretical and experimental constraints
\ Appendices
D Feynman diagrams in two-component DM model
4.2 Model

4.2.1 Scalar Sector
The scalar part of the Lagrangian is given by,
\
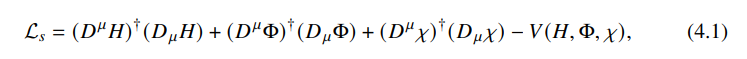
\ here the covariant derivative can be defined as
\
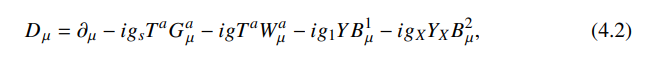
\ The scalar potential 𝑉(𝐻, Φ, 𝜒) is given by,
\
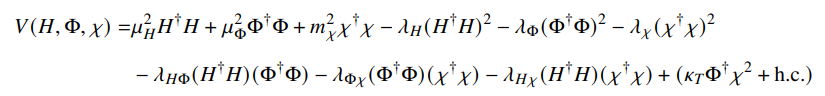
\ We parameterize the scalar fields as,
\
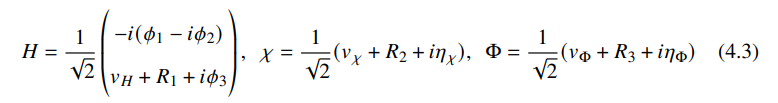
\

\

\

4.2.2 Gauge Sector

\

\

\

\

\ Masses of physical gauge bosons 𝐴, 𝑍 and 𝑍 ′ are given by,
\
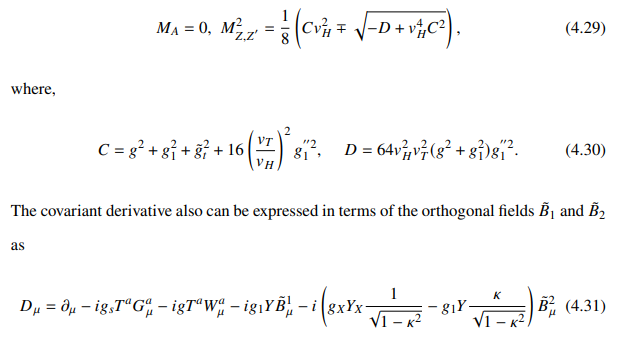
4.2.3 Yukawa Sector
The general form of the Yukawa interactions is given by,
\
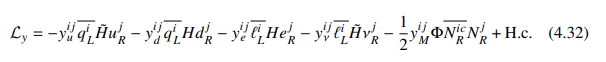
\ The last two terms are responsible for Dirac and Majorana masses of neutrinos.
4.2.4 Neutrino Mass
Relevant light neutrino masses will come from the fourth and fifth terms of Eq. 4.32. After the electroweak symmetry breaking, we can write the mass terms as,
\
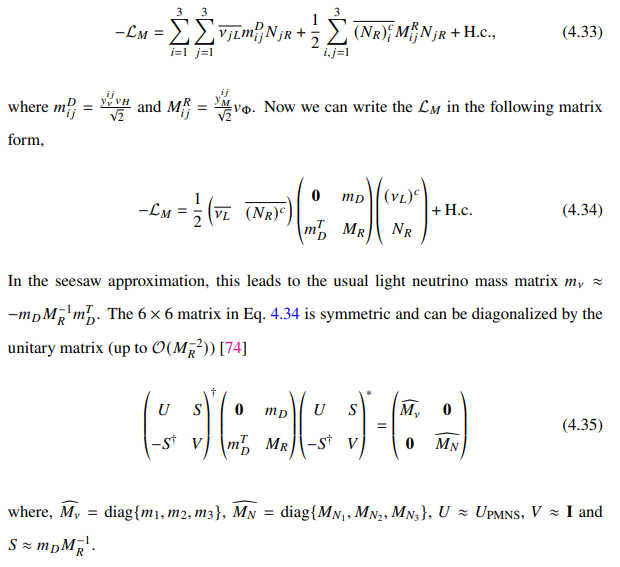
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
:::info Author:
(1) Shivam Gola, The Institute of Mathematical Sciences, Chennai.
:::
\
This content originally appeared on HackerNoon and was authored by Phenomenology Technology
Phenomenology Technology | Sciencx (2025-02-21T02:00:29+00:00) A Phenomenological Study of WIMP Models: Considering a BSM Framework. Retrieved from https://www.scien.cx/2025/02/21/a-phenomenological-study-of-wimp-models-considering-a-bsm-framework/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
