This content originally appeared on HackerNoon and was authored by Batching
Table of Links
3. Revisiting Normalization
3.1 Revisiting Euclidean Normalization
4 Riemannian Normalization on Lie Groups
5 LieBN on the Lie Groups of SPD Manifolds and 5.1 Deformed Lie Groups of SPD Manifolds
7 Conclusions, Acknowledgments, and References
\ APPENDIX CONTENTS
B Basic layes in SPDnet and TSMNet
C Statistical Results of Scaling in the LieBN
D LieBN as a Natural Generalization of Euclidean BN
E Domain-specific Momentum LieBN for EEG Classification
F Backpropagation of Matrix Functions
G Additional Details and Experiments of LieBN on SPD manifolds
H Preliminary Experiments on Rotation Matrices
I Proofs of the Lemmas and Theories in the Main Paper
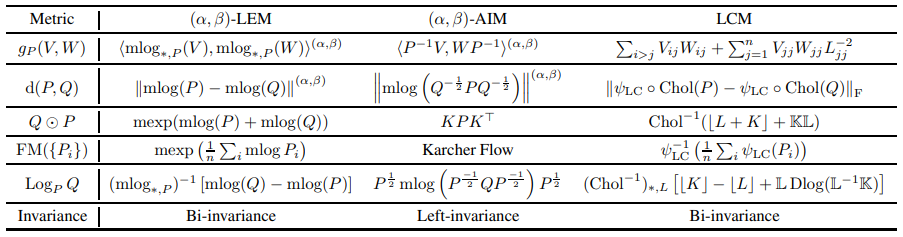
2 PRELIMINARIES
This section provides a brief review of the Lie group and the geometries of SPD manifolds. For more in-depth discussions, please refer to Tu (2011); Do Carmo & Flaherty Francis (1992).
\

\ A Lie group is a group and also a manifold. The most natural Riemannian metric on a Lie group is the left-invariant metric[1]. Similarly, one can define the right-invariant metric as Def. 2.2. A biinvariant Riemannian metric is the one with both left and right invariance. Given the analogous properties of left and right-invariant metrics, this paper focuses on left-invariant metrics.
\ The idea of pullback is ubiquitous in differential geometry and can be considered as a natural counterpart of bijection in the set theory.
\

\

\
\
:::info This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.
:::
[1] Left invariant metric always exists for every Lie group (Do Carmo & Flaherty Francis, 1992).
:::info Authors:
(1) Ziheng Chen, University of Trento;
(2) Yue Song, University of Trento and a Corresponding author;
(3) Yunmei Liu, University of Louisville;
(4) Nicu Sebe, University of Trento.
:::
\
This content originally appeared on HackerNoon and was authored by Batching
Batching | Sciencx (2025-02-22T03:34:54+00:00) A Brief Review of the Lie Group and the Geometries of SPD Manifolds. Retrieved from https://www.scien.cx/2025/02/22/a-brief-review-of-the-lie-group-and-the-geometries-of-spd-manifolds/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
