Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proof of the Main Theorem

Given the results of Lemmas 3.2 and 3.5, we expect our process to spend most of its time near a with σ small enough. In order to have more information about this behaviour, we introduce the following stopping times

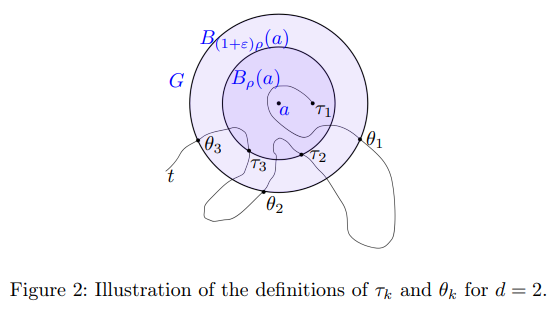
\ That gives us:

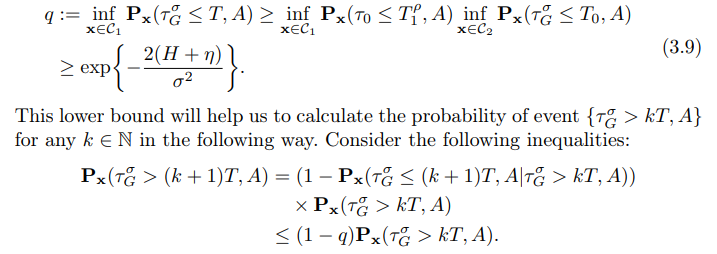
\ Therefore, by induction in k, we get:

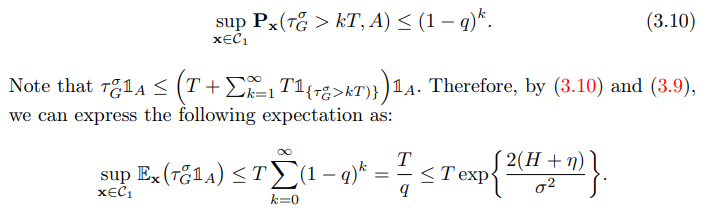
\ By Markov’s inequality, we get:

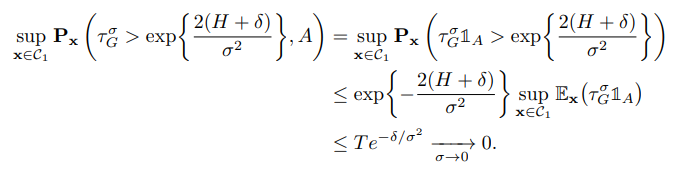
\ We remark that by Lemmas 3.1, 3.5 and derivations above, we have

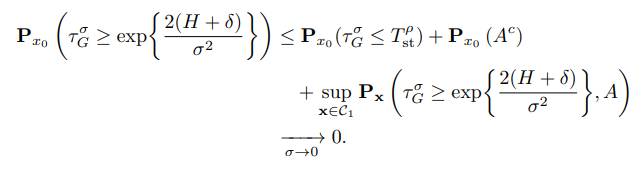
\ This concludes the proof.

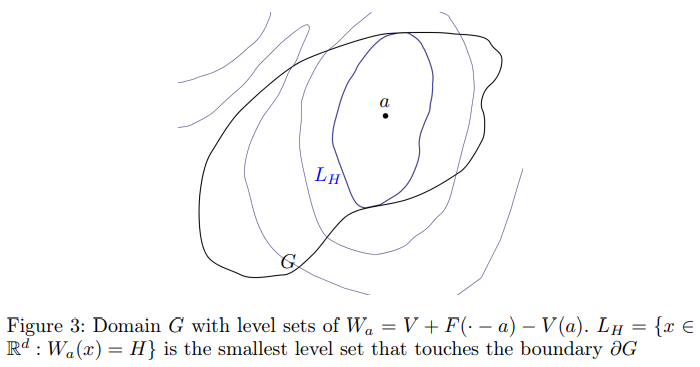
3.2.2 Exit-location

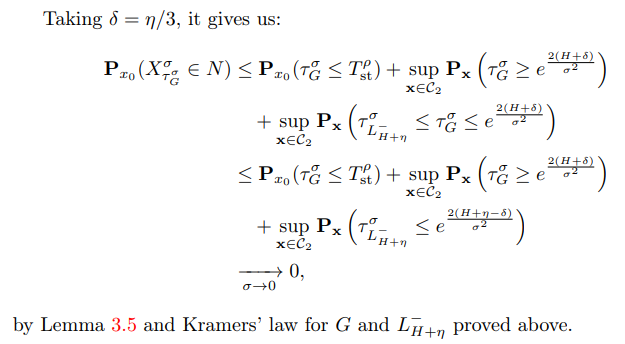
:::info This paper is available on arxiv under CC BY-SA 4.0 DEED license.

:::

:::info Authors:

(1) Ashot Aleksian, Université Jean Monnet, Institut Camille Jordan, 23, rue du docteur Paul Michelon, CS 82301, 42023 Saint-Étienne Cedex 2, France;

(2) Aline Kurtzmann, Université de Lorraine, CNRS, Institut Elie Cartan de Lorraine UMR 7502, Vandoeuvre-lès-Nancy, F-54506, France;

(3) Julian Tugaut, Université Jean Monnet, Institut Camille Jordan, 23, rue du docteur Paul Michelon, CS 82301, 42023 Saint-Étienne Cedex 2, France.

:::

This content originally appeared on HackerNoon and was authored by Class Path

Print Share Comment Cite Upload Translate Updates

APA

Class Path | Sciencx (2025-03-06T01:56:44+00:00) Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proof of the Main Theorem. Retrieved from https://www.scien.cx/2025/03/06/exit-problem-for-a-class-of-non-markov-processes-with-path-dependency-proof-of-the-main-theorem/

MLA

" » Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proof of the Main Theorem." Class Path | Sciencx - Thursday March 6, 2025, https://www.scien.cx/2025/03/06/exit-problem-for-a-class-of-non-markov-processes-with-path-dependency-proof-of-the-main-theorem/

HARVARD

Class Path | Sciencx Thursday March 6, 2025 » Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proof of the Main Theorem., viewed ,<https://www.scien.cx/2025/03/06/exit-problem-for-a-class-of-non-markov-processes-with-path-dependency-proof-of-the-main-theorem/>

VANCOUVER

Class Path | Sciencx - » Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proof of the Main Theorem. [Internet]. [Accessed ]. Available from: https://www.scien.cx/2025/03/06/exit-problem-for-a-class-of-non-markov-processes-with-path-dependency-proof-of-the-main-theorem/

CHICAGO

" » Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proof of the Main Theorem." Class Path | Sciencx - Accessed . https://www.scien.cx/2025/03/06/exit-problem-for-a-class-of-non-markov-processes-with-path-dependency-proof-of-the-main-theorem/

IEEE

" » Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proof of the Main Theorem." Class Path | Sciencx [Online]. Available: https://www.scien.cx/2025/03/06/exit-problem-for-a-class-of-non-markov-processes-with-path-dependency-proof-of-the-main-theorem/. [Accessed: ]

rf:citation

» Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proof of the Main Theorem | Class Path | Sciencx | https://www.scien.cx/2025/03/06/exit-problem-for-a-class-of-non-markov-processes-with-path-dependency-proof-of-the-main-theorem/ |

Please log in to upload a file.

There are no updates yet.
Click the Upload button above to add an update.

You must be logged in to translate posts. Please log in or register.

Table of Links

3.2 Proof of the main theorem

3.2.1 Kramers’ law

3.2.2 Exit-location

Related Posts