This content originally appeared on HackerNoon and was authored by Class Path
Table of Links
1.2 Some remarks on dynamics and initial condition
2.1 Establishing the LDP for the SID
2.2 Results related to the LDP
3.3 Proofs of auxiliary lemmas
4 Generalization and References
3.3 Proofs of auxiliary lemmas
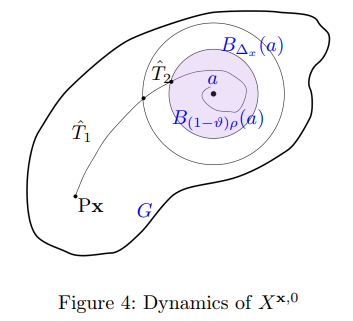
3.3.1 Proof of Lemma 3.1: Initial descent to the point of attraction

3.3.2 Proof of Lemma 3.2: Convergence of deterministic process towards a

\
\

\ Then, by Grönwall’s inequality:
\
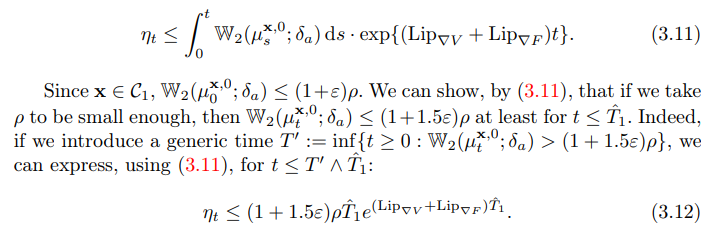
\

\ That guarantees exponentially fast convergence towards 0:
\
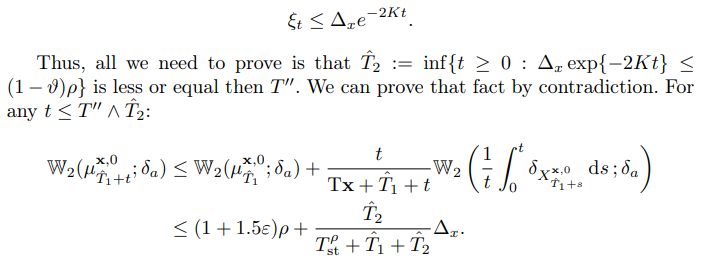
\
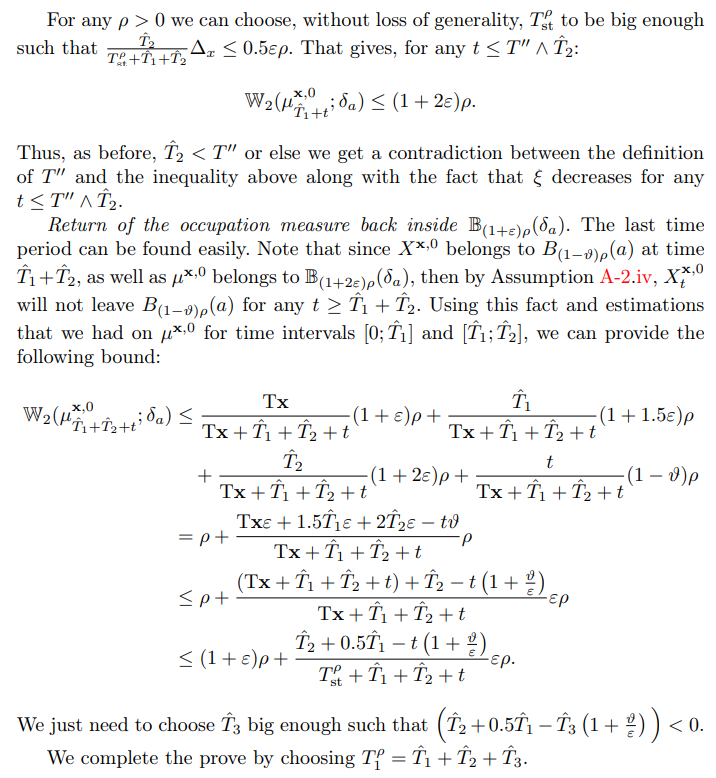
.3.3.3 Proof of Lemma 3.3: Attraction of stochastic process towards a
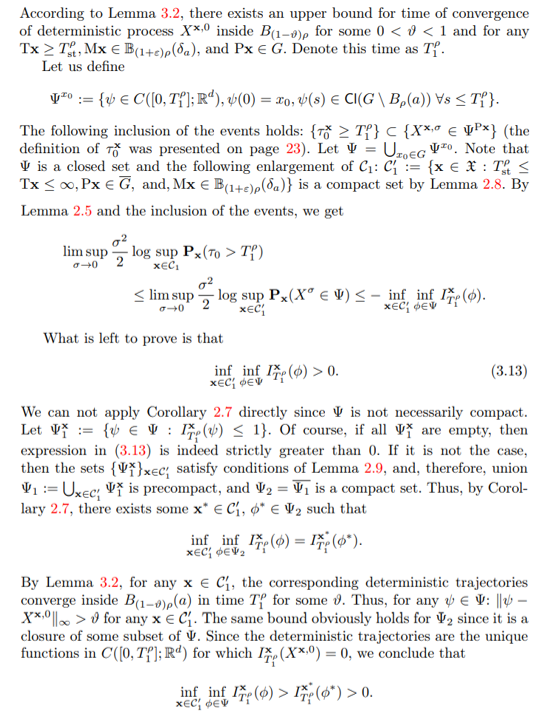
\ And this concludes the proof of the lemma.
3.3.4 Proof of Lemma 3.4: Behaviour in the annulus between Bρ(a) and ∂G

\
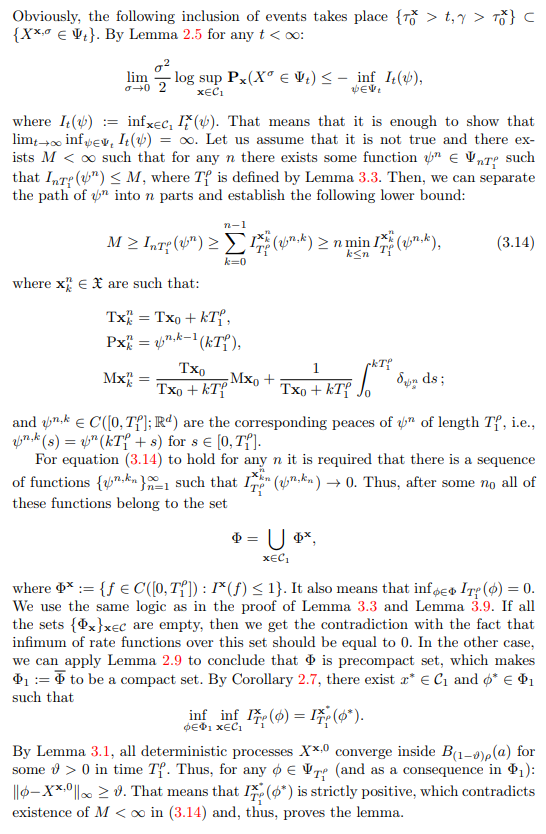
3.3.5 Proof of Lemma 3.5: Stabilization of the occupation measure

\ Proof. The proof of the following lemma follow the same logic as the one of Lemma 3.3.
\

\ We have to show now that
\

\ This completes the proof.
\ Now we are ready to prove Lemma 3.5 itself.
\

\ That gives us:
\

\
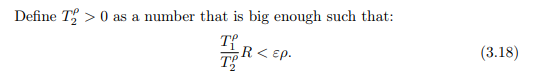
\ We recall that Lemma 3.9 establishes the following asymptotic behaviour for small σ:
\

\

\ Let us first deal with the term B. By (3.22), we have
\
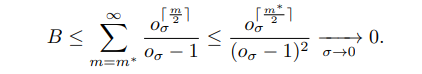
\ Consider now A. Separate each probability inside the sum the following way
\

\

3.3.6 Proof of Lemma 3.6: Exit before nearing a
First, we show that it is possible to establish a lower bound for
\
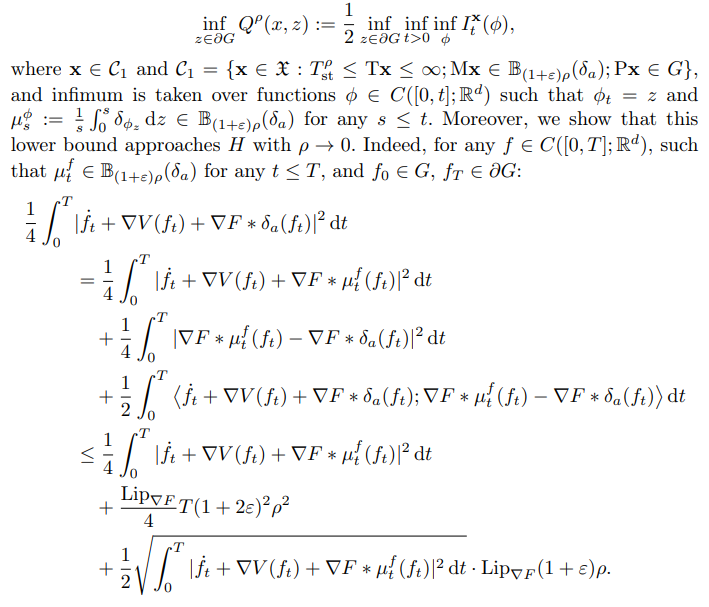
\

\ By Lemma 2.5,
\
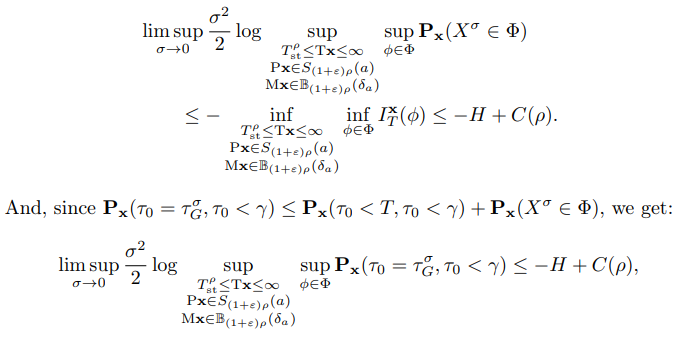
\ which proves the lemma by taking ρ → 0.
3.3.7 Proof of Lemma 3.7: Control of dynamics for small time intervals

\ Use the Jensen’s inequality, integrate the second part of the last integral over s, and get:
\
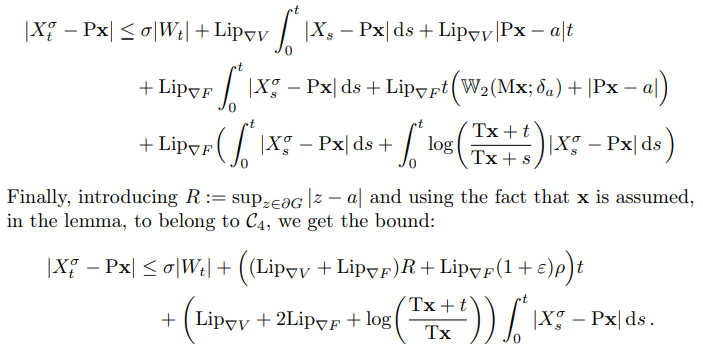
\ We apply Grönwall’s inequality and get:
\
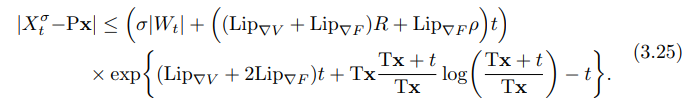
\ Thus, it follows that, for the absolute value of the Brownian motion itself,
\

\

\ Taking into account these remarks, we can now use the Schilder theorem [DZ10, Lemma 5.2.1] that provides the LDP for the path of the Brownian motion. Hence, for some fixed ϵ and 0 < T < 1:
\
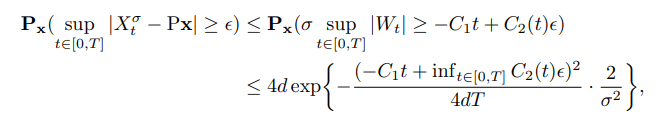
\ where d is the dimension of the space.
\ Note that for any ϵ > 0 the following limit holds:
\
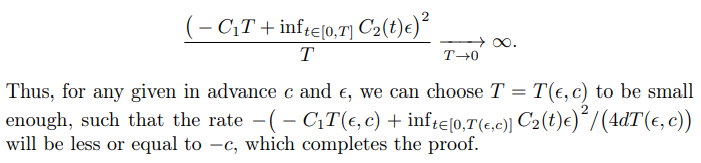
3.3.8 Proof of Lemma 3.8: Uniform lower bound for probability of exit from G

\

\
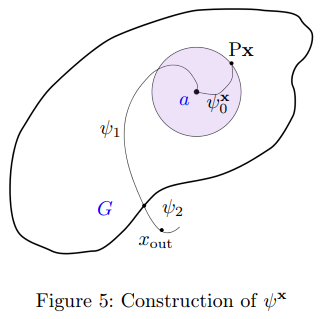
\

\
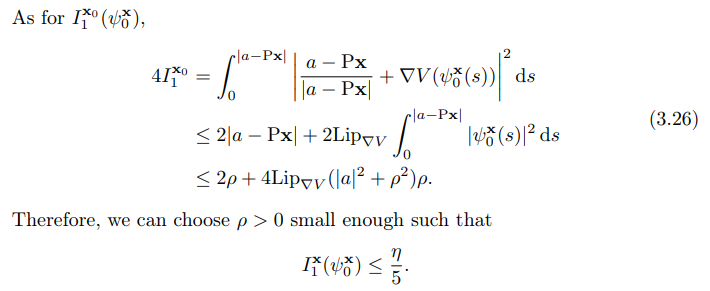
\

\

\

\

\
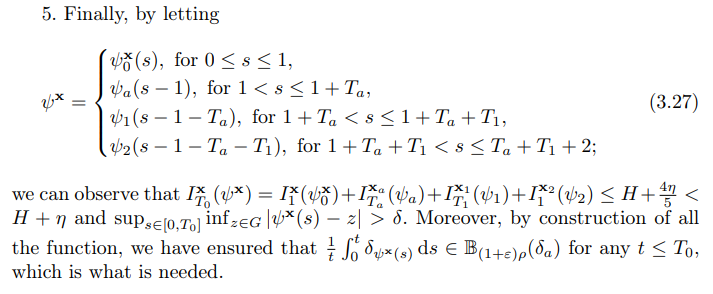
\
:::info This paper is available on arxiv under CC BY-SA 4.0 DEED license.
:::
:::info Authors:
(1) Ashot Aleksian, Université Jean Monnet, Institut Camille Jordan, 23, rue du docteur Paul Michelon, CS 82301, 42023 Saint-Étienne Cedex 2, France;
(2) Aline Kurtzmann, Université de Lorraine, CNRS, Institut Elie Cartan de Lorraine UMR 7502, Vandoeuvre-lès-Nancy, F-54506, France;
(3) Julian Tugaut, Université Jean Monnet, Institut Camille Jordan, 23, rue du docteur Paul Michelon, CS 82301, 42023 Saint-Étienne Cedex 2, France.
:::
\
This content originally appeared on HackerNoon and was authored by Class Path
Class Path | Sciencx (2025-03-06T02:18:57+00:00) Exit-Problem for a Class of Non-Markov Processes With Path Dependency: Proofs of Auxiliary Lemmas. Retrieved from https://www.scien.cx/2025/03/06/exit-problem-for-a-class-of-non-markov-processes-with-path-dependency-proofs-of-auxiliary-lemmas/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
