This content originally appeared on HackerNoon and was authored by Language Models (dot tech)
:::info Authors:
(1) Corby Rosset, Microsoft Research and Correspondence to corbyrosset@microsoft.com;
(2) Ching-An Cheng, Microsoft Research;
(3) Arindam Mitra, Microsoft Research;
(4) Michael Santacroce, Microsoft Research;
(5) Ahmed Awadallah, Microsoft Research and Correspondence to hassanam@microsoft.com;
(6) Tengyang Xie, Microsoft Research and Correspondence to tengyangxie@microsoft.com.
:::
Table of Links
2.1 RLHF Based on Reward Models
2.2 RLHF with General Preferences
3 Direct Nash Optimization and 3.1 Derivation of Algorithm 1
4 Practical Algorithm – Iterative Contrastive Self-Improvement
5 Experiments and 5.1 Experimental Setup
\ Appendix
A Extension to Regularized Preferences
C Additional Experimental Details
B Detailed Proofs
In this section, we provide detailed proofs for our theoretical results. Note that, the definitions and assumptions presented heavily adopts the ideas related to version space and concentrability from reinforcement learning theory literature (esp., Xie et al., 2021, 2023). Nevertheless, the descriptions provided herein are intentionally simplified to elucidate the core insights into the algorithmic design. A full and exhaustive theoretical analysis falls outside the primary scope of this paper. We now make the following definitions and assumptions.
\

\ Definition 2 can be viewed as a natural extension of concentrability from the (offline) reinforcement learning literature to our setup.
\

\ Proof of Theorem 2. We will now present the proof using the following two-step procedure.
\ Step 1: From regression with log loss to squared error bound. By standard results on the regression with the logarithmic loss, we know
\
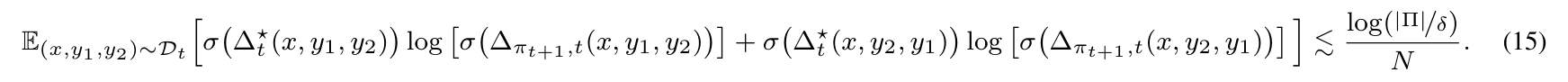
\ Note that similar results could also apply beyond finite Π. For simplicity, we omit the detailed discussion in our paper. For more in-depth discussions about regression with the logarithmic loss, the reader can refer to, e.g., Foster and Krishnamurthy (2021).
\

\

\

\ On the other hand, we have
\
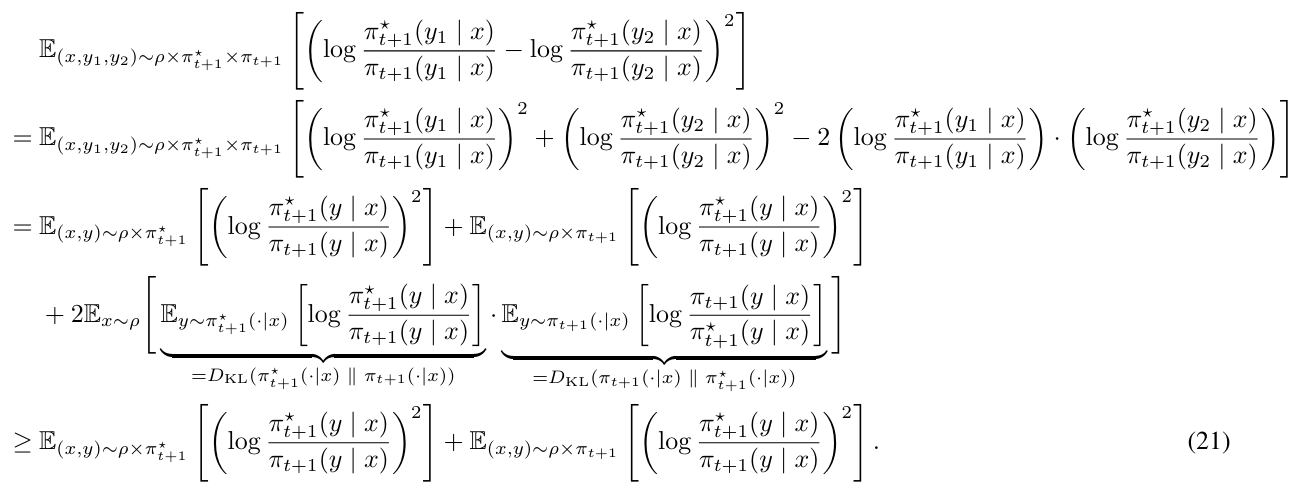
\

\

\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by Language Models (dot tech)
Language Models (dot tech) | Sciencx (2025-04-17T15:00:11+00:00) Understanding Concentrability in Direct Nash Optimization. Retrieved from https://www.scien.cx/2025/04/17/understanding-concentrability-in-direct-nash-optimization/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
