This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Table of Links
Translating To Sequent Calculus
Evaluation Within a Context
Insights
5.1 Evaluation Contexts are First Class
5.3 Let-Bindings are Dual to Control Operators
5.4 The Case-of-Case Transformation
5.5 Direct and Indirect Consumers
Conclusion, Data Availability Statement, and Acknowledgments
A. The Relationship to the Sequent Calculus
C. Operational Semantics of label/goto
3.2 Focusing on Evaluation in Core
Let us now come back to the problem in Core and find a solution for the stuck term ππΌ. + (ππ½. β (β2β, β4β; π½), β5β; πΌ). We know that we have to evaluate ππ½. β (β2β, β4β; π½) next and then somehow plug the intermediate result into the hole [Β·] in the producer ππΌ. + ( [Β·], β5β; πΌ). If we give the intermediate result the name π₯ and play around with cuts, π-bindings and πΛ bindings, we might discover that we can recombine all these parts in the following way:
\ ππΌ.β¨ππ½. β (β2β, β4β; π½) | ππ₯. Λ + (π₯, β5β; πΌ)β©
\ his term looks a bit mysterious, but the transformation corresponds roughly to what happens when we translate the term let π₯ = 2 β 4 in π₯ + 5 instead of (2 β 4) + 5 into Core. That is, we have lifted a subcomputation to the outside of the term we are evaluating. This kind of transformation is called focusing [Andreoli 1992; Curien and Munch-Maccagnoni 2010] and we use it to solve the problem with stuck terms in Core. We can see that it worked in our example because the term now fully evaluates to its normal form.
\ Example 3.1. The producer ππΌ.β¨ππ½. β (β2β, β4β; π½) | ππ₯. Λ + (π₯, β5β; πΌ)β© reduces as follows:
\ β¨ππ½. β (β2β, β4β; π½) | ππ₯. Λ + (π₯, β5β; β)β© β² β(β2β, β4β; ππ₯. Λ + (π₯, β5β; β))
\ β² β¨β8β | ππ₯. Λ + (π₯, β5β; β)β©
\ β² +(β8β, β5β; β) β² β¨β13β | ββ©
\ Once we have settled on focusing, we have another choice to make: Do we want to use this trick during the evaluation of a statement or as a preprocessing step before we start with the evaluation? These two alternatives are called dynamic and static focusing.
\ Dynamic Focusing With dynamic focusing [Wadler 2003] we add additional evaluation rules, usually called π-rules, to lift sub-computations to the outside of the statement we are evaluating.
\ Static Focusing For static focusing [Curien and Herbelin 2000] we perform a transformation on the code before we start evaluating it. This results in a focused normal form which is a subset of the syntax of Core that we have described so far.
\ Dynamic focusing is great for reasoning about the meaning of programs, but static focusing is more efficient if we are interested in compiling and running programs. For this reason, we only consider static focusing in what follows.
\
\ The complete rules for static focusing are presented in Definition 3.2. Most of these rules are only concerned with performing the focusing transformation on all subexpressions, but some of the clauses where something interesting happens are the clauses for binary operators:
\
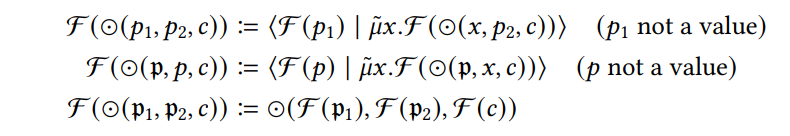
\ The first two clauses look for the arguments of the binary operator β which are not values and use the trick described above to lift them to the outside. Focusing is invoked recursively until the binary operator is only applied to values and the third clause comes into play. This third clause then applies the focusing transformation to all arguments of the binary operator. The clauses for constructors, destructors, ifz and calls to top-level definitions work in precisely the same way as those for binary operators. It is noteworthy that by focusing the producer arguments of destructors we guarantee that the evaluation rule for codata types can fire. If we had not required the producer arguments to be values in that rule (but only that the destructor is a covalue), we could easily introduce an unfocused term again by substituting a non-value for a variable.
\ The focusing transformation described in Definition 3.2 is not ideal since it creates a lot of administrative redexes. As an example, consider how the statement defining multβ from Example 2.7 is focused:
\ F (β¨π | case {Nil β β¨1 | π½β©, Cons(π₯, π₯π ) β ifz(π₯, β¨0 | πΌβ©, β(π₯, ππΎ .multβ(π₯π ; πΌ,πΎ); π½))}β©)
\ = β¨π | case {Nil β β¨1 | π½β©, Cons(π₯, π₯π ) β ifz(π₯, β¨0 | πΌβ©, β¨ππΎ .multβ(π₯π ; πΌ,πΎ) | ππ§. Λ β (π₯, π§; π½)β©)}β©
\ Focusing has introduced the administrative redex β¨ππΎ .multβ(π₯π ; πΌ,πΎ) | ππ§. Λ β (π₯, π§; π½)β© in the second statement of the ifz. After reducing this redex to multβ(π₯π ; πΌ, ππ§. Λ β (π₯, π§; π½)), we finally arrive at the result from the introduction. In the implementation, we solve this problem by statically reducing administrative redexes in a simplification step, but it is also possible to come up with a more elaborate definition of focusing which does not create them in the first place. Such an optimized focusing transformation is, however, much less transparent than the one we have described.
\
:::info Authors:
(1) David Binder, University of TΓΌbingen, Germany;
(2) Marco Tzschentke, University of TΓΌbingen, Germany;
(3) Marius Muller, University of TΓΌbingen, Germany;
(4) Klaus Ostermann, University of TΓΌbingen, Germany.
:::
:::info This paper is available on arxiv under CC BY 4.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Abstraction: Computer Science Discourse | Sciencx (2025-07-08T06:00:08+00:00) How Focusing Resolves Stuck Terms in Core Evaluation. Retrieved from https://www.scien.cx/2025/07/08/how-focusing-resolves-stuck-terms-in-core-evaluation/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.