This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Table of Links
Translating To Sequent Calculus
Evaluation Within a Context
Insights
5.1 Evaluation Contexts are First Class
5.3 Let-Bindings are Dual to Control Operators
5.4 The Case-of-Case Transformation
5.5 Direct and Indirect Consumers
Conclusion, Data Availability Statement, and Acknowledgments
A. The Relationship to the Sequent Calculus
C. Operational Semantics of label/goto
5.5 Direct and Indirect Consumers
As mentioned in the introduction, a natural competitor of sequent calculus as an intermediate representation is continuation-passing style (CPS). In CPS, reified evaluation contexts are represented by functions. This makes the resulting types of programs in CPS arguably harder to understand. There is, however, another advantage of sequent calculus over CPS as described by Downen et al. [2016]. The first-class representation of consumers in sequent calculus allows us to distinguish between two different kinds of consumers: direct consumers, i.e., destructors, and indirect consumers. In particular, this allows to chain direct consumers in Core in a similar way as in Fun.
\ Suppose we have a codata type with destructors get and set for getting and setting the value of a reference. Now consider the following chain of destructor calls on a reference 𝑟 in Fun
\ 𝑟 .set(3).set(4).get()
\ A compiler could use a user-defined custom rewrite rule for rewriting two subsequent calls to set into only the second call. In Core the above example looks as follows:
\ 𝜇𝛼.⟨𝑟 | set(3; set(4; get(𝛼)⟩
\ We still can immediately see the direct chaining of destructors and thus apply essentially the same rewrite rule. In CPS, however, the example would rather become
\ 𝜆𝑘. 𝑟 .set(3; 𝜆𝑠. 𝑠.set(4; 𝜆𝑡 . 𝑡 .get(𝑘)))
\ The chaining of the destructors becomes obfuscated by the indirections introduced by representing the continuations for each destructor as a function. To apply the custom rewrite rule mentioned above, it is necessary to see through the lambdas, i.e. the custom rewrite rule has to be transformed to be applicable.
5.6 Call-By-Value, Call-By-Name and Eta-Laws
In Section 2.2 we already pointed out the existence of statements ⟨𝜇𝛼.𝑠1 | 𝜇𝑥.𝑠 ˜ 2⟩ which are called critical pairs because they can a priori be reduced to either𝑠1 [𝜇𝑥.𝑠 ˜ 2/𝛼] or𝑠2 [𝜇𝛼.𝑠1/𝑥]. These critical pairs were already discussed by Curien and Herbelin [2000] when they introduced the 𝜆𝜇𝜇˜-calculus. One solution is to pick an evaluation order, either call-by-value (cbv) or call-by-name (cbn), that determines to which of the two statements we should evaluate, and in this paper we chose to always use the call-by-value evaluation order. The difference between these two choices has also been discussed by Wadler [2003]. Note that this freedom for the evaluation strategy is another advantage of sequent calculus over continuation-passing style, as the latter always fixes an evaluation strategy.
\ Which evaluation order we choose has an important consequence for the optimizations we are allowed to perform in the compiler. If we choose call-by-value, then we are not allowed to use all 𝜂-equalities for codata types, and if we use call-by-name, then we are not allowed to use all 𝜂-equalities for data types. Let us illustrate the problem in the case of codata types with the following example:
\ ⟨cocase {ap(𝑥; 𝛼) ⇒ ⟨𝜇𝛽.𝑠1 | ap(𝑥; 𝛼)⟩} | 𝜇𝑥.𝑠 ˜ 2⟩ ≡𝜂 ⟨𝜇𝛽.𝑠1 | 𝜇𝑥.𝑠 ˜ 2⟩
\ We assume that 𝑥 and 𝛼 do not appear free in 𝑠1. The 𝜂-transformation is just the ordinary 𝜂-law for functions but applied to the representation of functions as codata types. The statement on the left-hand side reduces the 𝜇˜ first under both call-by-value and call-by-name evaluation order, i.e.
\
\
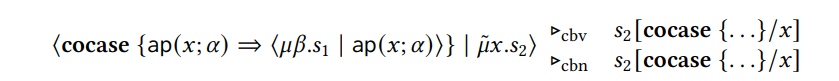
\ \ The right-hand side of the 𝜂-equality, however, reduces the 𝜇 first under call-by-value evaluation order, i.e.
\
\
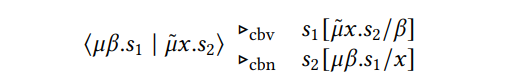
\ \ Therefore, the 𝜂-equality is only valid under call-by-name evaluation order. This example shows that the validity of applying this 𝜂-rule as an optimization depends on whether the language uses call-by-value or call-by-name. If we instead used a data type such as Pair, a similar 𝜂-reduction would only give the same result as the original statement when using call-by-value.
5.7 Linear Logic and the Duality of Exceptions
We have introduced the data type Pair(𝜎, 𝜏) and the codata type LPair(𝜎, 𝜏) as two different ways to formalize tuples. The data type Pair(𝜎, 𝜏) is defined by the constructor Tup whose arguments are evaluated eagerly, so this type corresponds to strict tuples in languages like ML or OCaml. The codata type LPair(𝜎, 𝜏) is a lazy pair which is defined by its two projections fst and snd, and only when we invoke the first or second projection do we start to compute its contents. This is closer to how tuples behave in a lazy language like Haskell.
\ Linear logic [Girard 1987; Wadler 1990] adds another difference to these types. In linear logic we consider arguments as resources which cannot be arbitrarily duplicated or discarded; every argument to a function has to be used exactly once. If we follow this stricter discipline, then we have to distinguish between two different types of pairs: In order to use a pair 𝜎 ⊗ 𝜏 (pronounced “times” or “tensor”), we have to use both the 𝜎 and the 𝜏, but if we want to use a pair 𝜎 & 𝜏 (pronounced “with”), we must choose to either use the 𝜎 or the 𝜏. It is now easy to see that the type 𝜎 ⊗ 𝜏 from linear logic corresponds to the data type Pair(𝜎, 𝜏), since when we pattern match on this type we get two variables in the context, one for 𝜎 and one for 𝜏. The type 𝜎 & 𝜏 similarly corresponds to the type LPair(𝜎, 𝜏) which we use by invoking either the first or the second projection, consuming the whole pair.
\
\

\
\
\

\
:::info Authors:
(1) David Binder, University of Tübingen, Germany;
(2) Marco Tzschentke, University of Tübingen, Germany;
(3) Marius Muller, University of Tübingen, Germany;
(4) Klaus Ostermann, University of Tübingen, Germany.
:::
:::info This paper is available on arxiv under CC BY 4.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Abstraction: Computer Science Discourse | Sciencx (2025-07-09T07:00:04+00:00) Sequent Calculus vs CPS: A Compiler’s Perspective on Consumers and Evaluation Strategies. Retrieved from https://www.scien.cx/2025/07/09/sequent-calculus-vs-cps-a-compilers-perspective-on-consumers-and-evaluation-strategies/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
