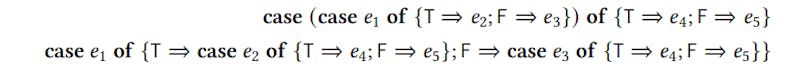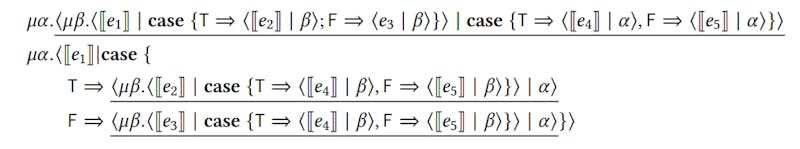This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Table of Links
Translating To Sequent Calculus
Evaluation Within a Context
Insights
5.1 Evaluation Contexts are First Class
5.3 Let-Bindings are Dual to Control Operators
5.4 The Case-of-Case Transformation
5.5 Direct and Indirect Consumers
Conclusion, Data Availability Statement, and Acknowledgments
A. The Relationship to the Sequent Calculus
C. Operational Semantics of label/goto
5.3 Let-Bindings are Dual to Control Operators
The label construct in Fun is translated to a ๐-binding in Core. Also, when considering the typing rule for label ๐ผ {๐ก } in Section 4.1, we can see that it directly corresponds to typing a ๐-binding with the label ๐ผ being the bound covariable. Similarly, a let-binding is translated to a ๐ห-binding and typing a let-binding in Fun closely corresponds to typing a ๐ห-term in Core. This way, labels and let-bindings are dual to each other, the same way ๐ and ๐ห are. The duality can be extended to other control operators such as call/cc.
\ As it turns out, the label construct is very closely related to call/cc. There are in fact only two differences. First, label ๐ผ {๐ก } has the binder ๐ผ for the continuation built into the construct, just as the variation of call/cc named let/cc (which Reynolds [1972] called escape). The second, and more important difference is that the invocation of the continuation captured by label ๐ผ {๐ก } happens through an explicit language construct goto(๐ก; ๐ผ). This makes it easy to give a translation to Core as we can simply insert another ๐-binding to discard the remaining continuation at exactly the place where the captured continuation is invoked. In contrast, with call/cc and let/cc the continuation is applied in the same way as a normal function, making it necessary to redefine the variable the captured continuation is bound to when translating to Core. This obscures the duality to let-bindings which is so evident for label and goto.
\ To see this, here is a translation of let/cc ๐ ๐ก to Core
\ [let/cc ๐ ๐ก] โ ๐๐ผ.โจcocase {ap(๐ฅ, ๐ฝ) โ โจ๐ฅ | ๐ผโฉ} | ๐๐. ห โจ[๐ก] | ๐ผโฉโฉ
\ The essence of the translation still is that the current continuation is captured by the outer ๐ and bound to ๐ผ. But now we also have to transform this ๐ผ into a function (the cocase here) which discards its context (here bound to ๐ฝ) and bind this function to ๐, which is done using ๐ห. For call/cc, the duality is even more obscured, as there the binder for the continuation is hidden in the function which call/cc is applied to. For the translation, this function must then be applied to the above cocase and the captured continuation ๐ผ, resulting in the following term (cf. also [Miquey 2019]).
\ [call/cc ๐] โ ๐๐ผ.โจ[๐ ] | ap(cocase {ap(๐ฅ, ๐ฝ) โ โจ๐ฅ | ๐ผโฉ}, ๐ผ)โฉ
\ Other control operators for undelimited continuations can be translated in a similar way. For example, consider Felleisenโs C [Felleisen et al. 1987]. The difference to call/cc is that C discards the current continuation if it is not invoked somewhere in the term C is applied to, whereas call/cc leaves it in place and thus behaves as a no-op if the captured continuation is never invoked. The only change that needs to be made in the translation to Core is that the top-level continuation โ has to be used for the outer cut instead of using the captured continuation. This is most easily seen for a variation of C which has the binder for the continuation built into the operator and where the invocation of the continuation is explicit, similar to label/goto. Calling this variation labelC, we obtain the following translation
\ [labelC ๐ผ {๐ก }] โ ๐๐ผ.โจ[๐ก] | โโฉ
\ Here the duality to let-bindings is evident again. The translation for C itself is then obtained in the same way as for call/cc
\ [C ๐ ] โ ๐๐ผ.โจ[๐ ] | ap(cocase {ap(๐ฅ, ๐ฝ) โ โจ๐ฅ | ๐ผโฉ}, โ)โฉ
5.4 The Case-of-Case Transformation
One important transformation in functional compilers is the case-of-case transformation. Maurer et al. [2017] give the following example of this transformation. The term
\n
if (if ๐1 then ๐2 else ๐3) then ๐4 else ๐5
\n
can be replaced by the term
\n
if ๐1 then (if ๐2 then ๐4 else ๐5) else (if ๐3 then ๐4 else ๐5).
\n
Logicians call these kinds of transformations commutative conversions, and they play an important role in the study of the sequent calculus. But as Maurer et al. [2017] show, they are also important for compiler writers who want to generate efficient code.
\n
In the ๐๐๐ห-calculus, commuting conversions donโt have to be implemented as a special compiler pass. They fall out for free as a special instance of ๐-reductions! Let us illustrate this point by translating Maurer et al.โs example into the ๐๐๐ห-calculus. First, let us translate the two examples using pattern-matching syntax:
\n
\
\ Let us now translate these two terms into the ๐๐๐ห-calculus:
\n
\
\ \n
We can see that just by reducing all of the underlined redexes we reduce both of these examples to the same term.
:::info Authors:
(1) David Binder, University of Tรผbingen, Germany;
(2) Marco Tzschentke, University of Tรผbingen, Germany;
(3) Marius Muller, University of Tรผbingen, Germany;
(4) Klaus Ostermann, University of Tรผbingen, Germany.
:::
:::info This paper is available on arxiv under CC BY 4.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Abstraction: Computer Science Discourse | Sciencx (2025-07-09T06:12:42+00:00) Why Compiler Writers Care About Case-of-Case. Retrieved from https://www.scien.cx/2025/07/09/why-compiler-writers-care-about-case-of-case/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.