This content originally appeared on HackerNoon and was authored by Extrapolate
:::info Authors:
(1) Haolong Li, Tongji Universiy and work done during internship at ByteDance (furlongli322@gmail.com);
(2) Yu Ma, Seed Foundation, ByteDance (mayu.1231@bytedance.com);
(3) Yinqi Zhang, East China Normal University and work done during internship at ByteDance (zhang.inch@gmail.com);
(4) Chen Ye (Corresponding Author), ESSC Lab, Tongji Universiy (yechen@tongji.edu.cn);
(5) Jie Chen, Seed Foundation, ByteDance and a Project Leader (chenjiexjtu@gmail.com).
:::
Table of Links
2 Problem Definition
2.1 Arithmetical Puzzle Problem
4 Experiments
5 Conclusion and Acknowledgements
7 Ethics Statement and References
\ A Appendix
A.2 Evaluation of the Base Model
A.4 Visualization of the Proposed Puzzle
A.1 Hyperparameter Settings
In the SFT stage, we follow common fine-tuning hyperparameter settings for our model. We set learning rate to 1e−4 and adopt the cosine learning rate scheduler. We use low-rank adaptation (LoRA) tuning with a rank of 5, α of 32, and dropout of 0.05. And we employ Adamw optimizer with β1 = 0.9, β2 = 0.95 and ϵ = 1e − 9. Eight NVIDIA A100-SXM4-80GB GPUs are used to train the model with a batch size of 50 and the maximum epoch set to 5. Detailed settings are listed in Table 3.
\
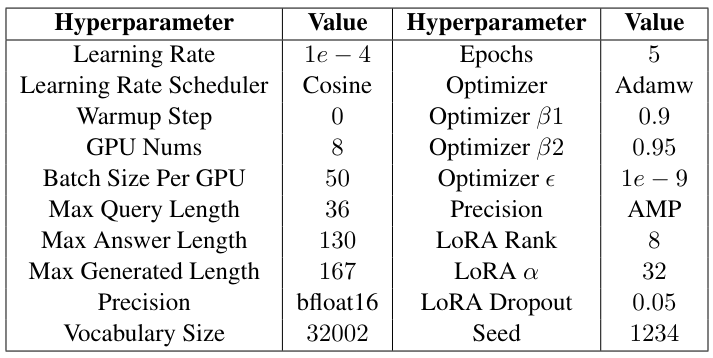
\
A.2 Evaluation of the Base Model
We evaluate the base model (open-llama-3B) on the proposed arithmetical puzzle problem. As shown in Table 4 and Table 5, with either the few-shot prompting (2-Shot, 8-Shot) or Chain-of-Thought (CoT), the base model performs poorly on the puzzle. We propose this is due to the symbolic form of our prompt, the model needs to understand the underlying pattern in order to solve the arithmetical puzzle. Without fine-tuning on the synthetic data, the model may struggle to comprehend such type of prompt.
\
\
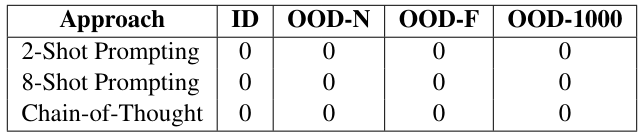
\
\
\

\ \ We further test several open-source (Llama-2-7B (Touvron et al., 2023a), Deepseek-Coder-33B (Guo et al., 2024)) and closed-source models (GPT4 (Achiam et al., 2023)) with few-shot prompting. As shown in Table 6, these models also perform poorly on our benchmarks. In Table 7, we provide an example of the CoT prompting and the generated responses from these models.
\
\

\
\
\
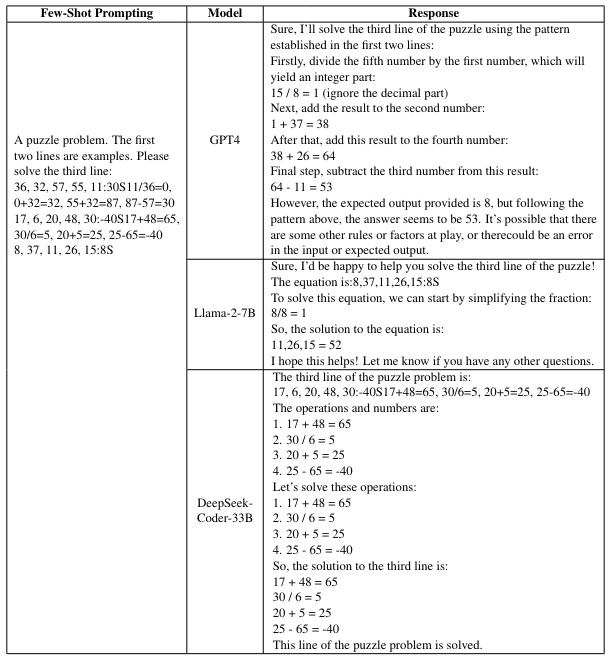
\ \ As shown in Table 7, Llama-2-7B fails to understand the requirement of the puzzle and just outputs two meaningless equations. Deepseek-Coder-33B treats the second example in few-shot prompting as the puzzle, and repeats the same calculations three times. It seems that GPT4 has well understood the prompt and used all the candidate integers only once, the calculations within the generated response are all right, while the solution is wrong. Actually, such kind of problem is very challenging, as the model needs to infer the requirement of the puzzle from the provided examples and then figure out the correct solution.
\
A.3 Case Study
\

\
A.4 Visualization of the Proposed Puzzle
\
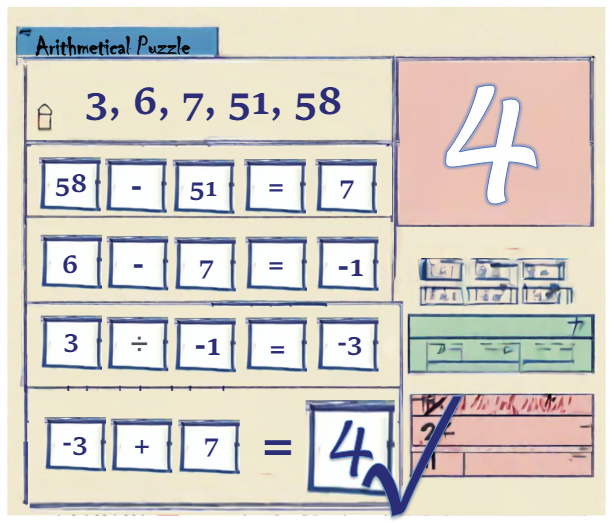
\ \ \
:::info This paper is available on arxiv under CC BY-NC-SA 4.0 Deed (Attribution-Noncommercial-Sharelike 4.0 International) license.
:::
\
This content originally appeared on HackerNoon and was authored by Extrapolate
Extrapolate | Sciencx (2025-08-23T16:36:12+00:00) Why LLMs Struggle with Arithmetic Puzzles. Retrieved from https://www.scien.cx/2025/08/23/why-llms-struggle-with-arithmetic-puzzles/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
