This content originally appeared on HackerNoon and was authored by Rebalancing
:::info Authors:
(1) Kaier Liang, with the Mechanical Engineering and Mechanics Department at Lehigh University, PA, USA;
(2) Cristian-Ioan Vasile, with the Mechanical Engineering and Mechanics Department at Lehigh University, PA, USA.
:::
Table of Links
VI. Conclusions and References
V. SIMULATION
In this section, we present the simulation results to demonstrate the performance of distributed fair assignment and the rebalancing scheme.
\
A. Simulation Specifications
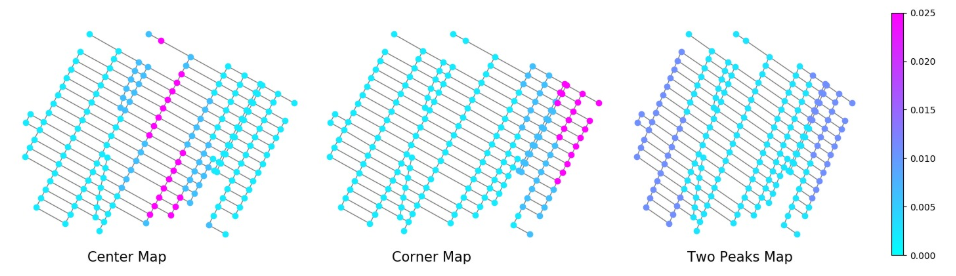
The road map for the simulation is used as the MidManhattan map, which contains 184 nodes, and the weights for every edge are acquired by real travel duration from taxi driving data [25]. We varied the request generation probabilities and the number of requests to evaluate the fairness performance of the system. Three different maps were used for the simulations, namely the center map, corner map, and two peaks map, with request generation probabilities as shown in Fig. 2. These maps are characterized by high probability areas where requests are more likely to be generated. So that it can reflect the uneven distribution of requests in real-life scenarios.
\ The simulation duration is set to 1000 seconds with varying the number of vehicles and requests. The initial positions of all vehicles are generated in a uniform distribution. The scLTL formulas for the requests are generated from the following scLTL pattern stochastically.
\

\ Throughout the simulation, we perform the auction and rebalancing every 10 seconds. Additionally, we set the maximum waiting time and delay time to 40 and 100 seconds.
\
\
\
\
B. Simulation Results
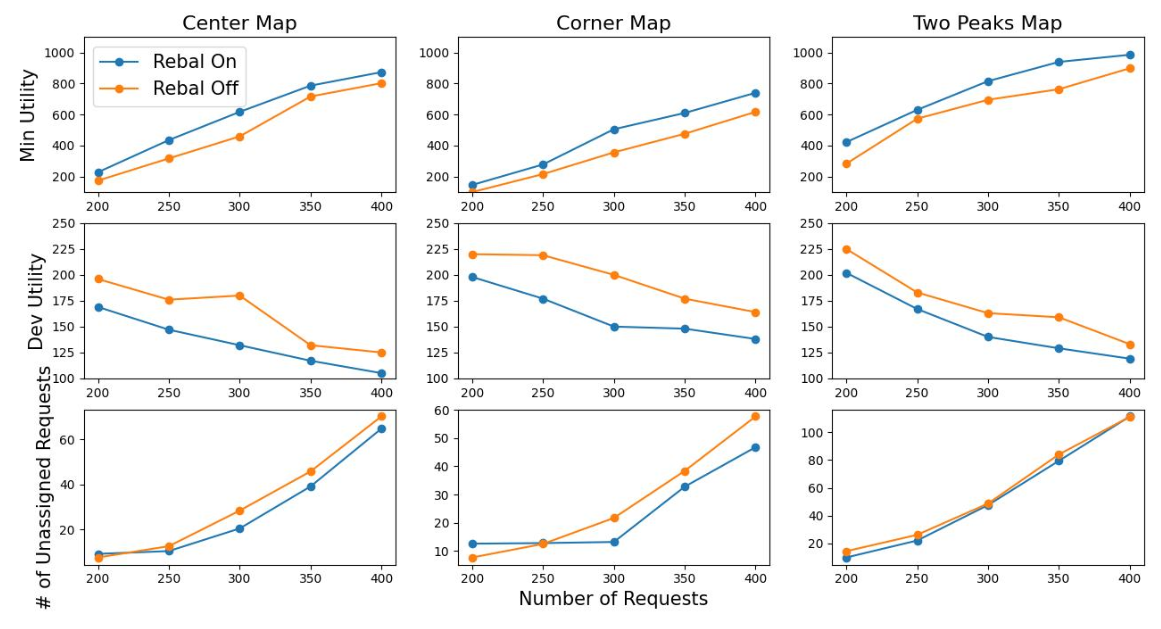
In the simulation results shown in Fig. 2, we consider 20 vehicles and a varying number of requests from 200 to 400 to demonstrate the effect of the rebalancing strategy. Each data point in the figure is the average result of 20 simulations. The fairness is compared using the minimum and deviation utility. Fig. 2 shows we can increase the minimum utility and decrease the deviation utility consistently without degenerating the serving rate in all three map settings.
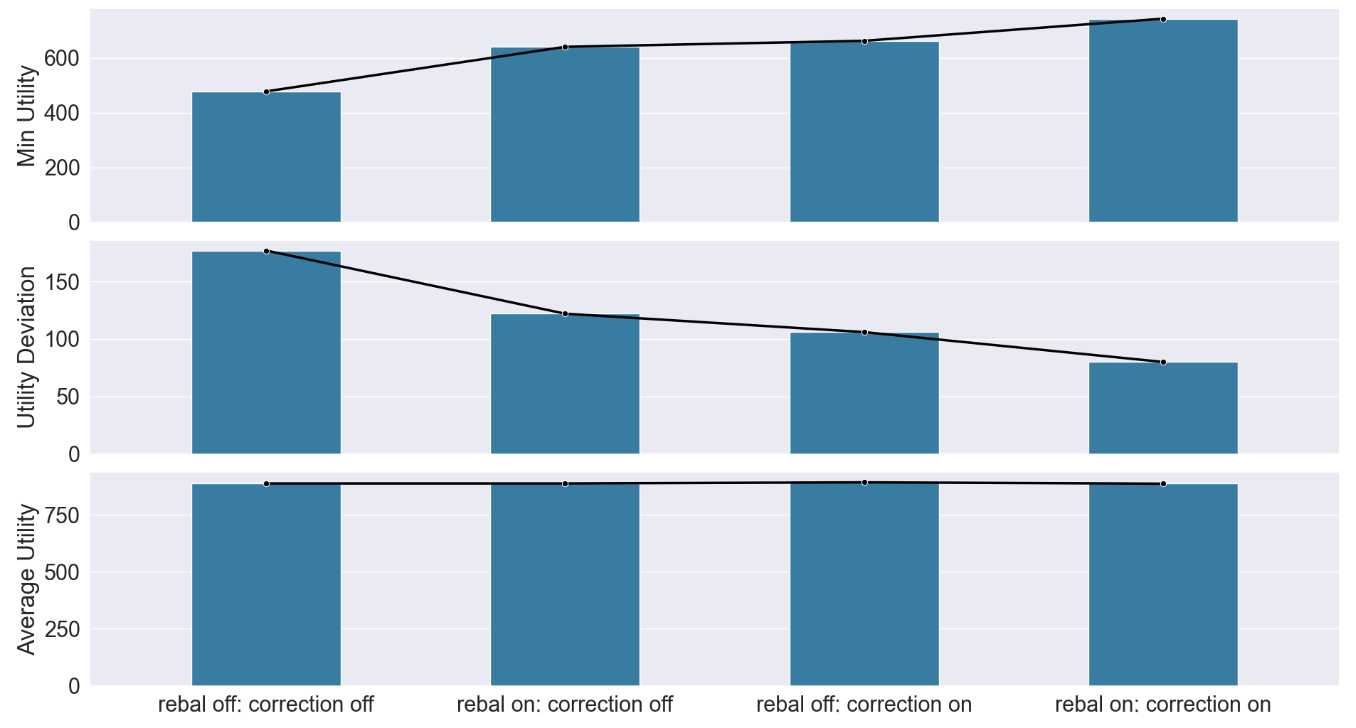
\ Fig. 3 shows the comparison between the planning with and without weight correction and rebalancing settings. We can see the improvement of introducing rebalancing or the weight correction from the two fairness criteria; the settings that adopt the rebalancing or weight correction can increase the minimum utility and decrease the deviation utility. And the setting performs best when it uses the rebalancing and the weight correction together.
\ In Fig. 3, we also notice that using balancing or weight correction does not affect the average utility. This suggests that although we cannot increase the total utility for the entire system, we can adjust the utility distribution in a fair way by increasing the minimum utility and decreasing the deviation.
\
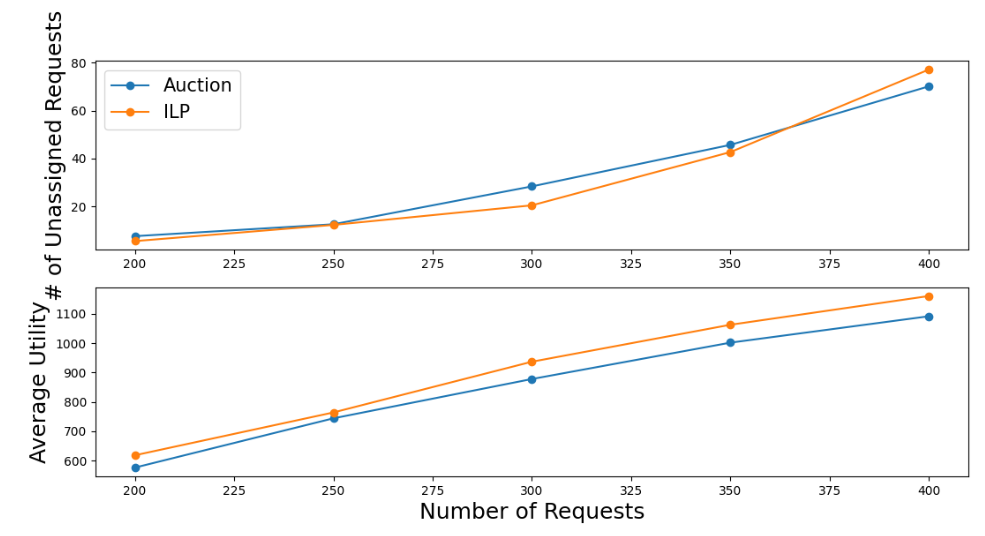
\ Comparison with the centralized approach: here we present the performance comparison between the auction algorithm and centralized algorithm using ILP [26]. Although both algorithms can obtain the optimal solution, the algorithms’ implementations are different. First, the ILP setting allows more than one request to be assigned together at one step due to the optimization nature, whereas the auction algorithm can only assign one request to one vehicle at one-time. Furthermore, since both methods are run continuously throughout the simulation, it is not possible to obtain the global optimal solution. Therefore, the current optimal solution does not imply the global property, as future events cannot be predicted at the current time step.
\ For the comparison shown in Fig. 4, we compare the auction and ILP methods for the setting with 20 vehicles and a varying number of requests. While both approaches are to minimize the traveling time, this is not easy to quantify and compare directly. Thus, we evaluate the average utility and the number of unassigned requests. The average utility and the number of unassigned requests capture the running quality from the requests and vehicles’ perspectives. For the comparison, we used both the auction and ILP settings without rebalancing and weight correction. We see that the two approaches perform very similarly which is expected.
\
VI. CONCLUSIONS
In conclusion, this paper presents a novel approach to the problem of fair assignment and rebalancing in MobilityOn-Demand systems. Our proposed distributed assignment method reduces the need for a central authority for coordination. The introduction of the rebalancing scheme leads to a fairer distribution of requests for vehicles, as demonstrated by an increase in the minimum utility and a decrease in the utility deviation compared to the baseline. By modeling requests using temporal logic formulas, our approach accommodates complex demand patterns. The results of our study demonstrate the efficacy of the proposed method in achieving fairer vehicle assignment in Mobility-On-Demand systems.
\
REFERENCES
[1] T. Teubner and C. M. Flath, “The economics of multi-hop ride sharing,” Business & Information Systems Engineering, vol. 57, no. 5, pp. 311–324, 2015.
\ [2] S. Liyanage, H. Dia, R. Abduljabbar, and S. A. Bagloee, “Flexible mobility on-demand: An environmental scan,” Sustainability, vol. 11, no. 5, p. 1262, 2019.
\ [3] Y. Cao, S. Wang, and J. Li, “The optimization model of ride-sharing route for ride hailing considering both system optimization and user fairness,” Sustainability, vol. 13, no. 2, p. 902, 2021.
\ [4] M. D. Aleksandrov, “Fair division meets vehicle routing: Fairness for drivers with monotone profits,” in 2022 IEEE Intelligent Vehicles Symposium (IV), pp. 915–920, IEEE, 2022.
\ [5] L. Foti, J. Lin, O. Wolfson, and N. D. Rishe, “The nash equilibrium among taxi ridesharing partners,” in ACM SIGSPATIAL Intl Conf on Advances in Geographic Information Systems, pp. 1–4, 2017.
\ [6] Y. Lin, W. Li, F. Qiu, and H. Xu, “Research on optimization of vehicle routing problem for ride-sharing taxi,” Procedia-Social and Behavioral Sciences, vol. 43, pp. 494–502, 2012.
\ [7] M. W. Levin, “Congestion-aware system optimal route choice for shared autonomous vehicles,” Transportation Research Part C: Emerging Technologies, vol. 82, pp. 229–247, 2017.
\ [8] V. Pandey, J. Monteil, C. Gambella, and A. Simonetto, “On the needs for maas platforms to handle competition in ridesharing mobility,” Transportation Research Part C: Emerging Technologies, vol. 108, pp. 269–288, 2019.
\ [9] A. Simonetto, J. Monteil, and C. Gambella, “Real-time city-scale ridesharing via linear assignment problems,” Transportation Research Part C: Emerging Technologies, vol. 101, pp. 208–232, 2019.
\ [10] J. Wen, J. Zhao, and P. Jaillet, “Rebalancing shared mobility-ondemand systems: A reinforcement learning approach,” in Intl Conf on Intelligent Transportation Systems, pp. 220–225, IEEE, 2017.
\ [11] S. L. Smith, M. Pavone, M. Schwager, E. Frazzoli, and D. Rus, “Rebalancing the rebalancers: Optimally routing vehicles and drivers in mobility-on-demand systems,” in 2013 American Control Conference, pp. 2362–2367, IEEE, 2013.
\ [12] K. Spieser, S. Samaranayake, W. Gruel, and E. Frazzoli, “Sharedvehicle mobility-on-demand systems: a fleet operator’s guide to rebalancing empty vehicles,” in Transportation Research Board 95th Annual Meeting, no. 16-5987, Transportation Research Board, 2016.
\ [13] J. Tumova, S. Karaman, C. Belta, and D. Rus, “Least-violating planning in road networks from temporal logic specifications,” in Intl Conf on Cyber-Physical Systems, pp. 1–9, IEEE, 2016.
\ [14] C. I. Vasile and C. Belta, “Sampling-based temporal logic path planning,” in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 4817–4822, IEEE, 2013.
\ [15] H. Kress-Gazit, G. E. Fainekos, and G. J. Pappas, “Temporal-logicbased reactive mission and motion planning,” IEEE transactions on robotics, vol. 25, no. 6, pp. 1370–1381, 2009.
\ [16] E. Plaku and S. Karaman, “Motion planning with temporal-logic specifications: Progress and challenges,” AI communications, vol. 29, no. 1, pp. 151–162, 2016.
\ [17] D. Kamale, E. Karyofylli, and C.-I. Vasile, “Automata-based optimal planning with relaxed specifications,” in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 6525–6530, 2021.
\ [18] X. Ding, S. L. Smith, C. Belta, and D. Rus, “Optimal control of markov decision processes with linear temporal logic constraints,” IEEE Transactions on Automatic Control, vol. 59, no. 5, pp. 1244– 1257, 2014.
\ [19] G. A. Cardona, D. Saldana, and C.-I. Vasile, “Planning for modular ˜ aerial robotic tools with temporal logic constraints,” in 2022 IEEE 61st Conference on Decision and Control (CDC), pp. 2878–2883, 2022.
\ [20] E. M. Wolff, U. Topcu, and R. M. Murray, “Optimization-based trajectory generation with linear temporal logic specifications,” in 2014 IEEE International Conference on Robotics and Automation (ICRA), pp. 5319–5325, IEEE, 2014.
\ [21] C. Belta, B. Yordanov, and E. A. Gol, Formal methods for discretetime dynamical systems, vol. 15. Springer, 2017.
\ [22] C. Baier and J. Katoen, Principles of model checking. MIT Press, 2008. [23] T. Latvala, “Efficient Model Checking of Safety Properties,” in 10th International SPIN Workshop, Model Checking Software, pp. 74–88, Springer, 2003.
\ [24] A. Duret-Lutz, “Manipulating LTL formulas using Spot 1.0,” in Intl Symposium on Automated Technology for Verification and Analysis, vol. 8172 of LNCS, (Hanoi, Vietnam), pp. 442–445, Springer, 2013.
\ [25] J. Alonso-Mora, S. Samaranayake, A. Wallar, E. Frazzoli, and D. Rus, “On-demand high-capacity ride-sharing via dynamic trip-vehicle assignment,” Proceedings of the National Academy of Sciences, vol. 114, no. 3, pp. 462–467, 2017.
\ [26] K. Liang and C.-I. Vasile, “Fair planning for mobility-on-demand with temporal logic requests,” in 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 1283–1289, IEEE, 2022.
\ [27] S. J. Brams, S. J. Brams, and A. D. Taylor, Fair Division: From cakecutting to dispute resolution. Cambridge University Press, 1996.
\ [28] H. P. Young, Equity: in theory and practice. Princeton University Press, 1995.
\ [29] D. P. Bertsekas, “The auction algorithm: A distributed relaxation method for the assignment problem,” Annals of operations research, vol. 14, no. 1, pp. 105–123, 1988.
\ [30] M. Sniedovich, “Dijkstra’s algorithm revisited: the dynamic programming connexion,” Control and cybernetics, vol. 35, no. 3, pp. 599–620, 2006.
\
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\
This content originally appeared on HackerNoon and was authored by Rebalancing
Rebalancing | Sciencx (2025-08-25T21:47:35+00:00) Simulation Results of Distributed Fair Assignment and Rebalancing in Mobility‑On‑Demand. Retrieved from https://www.scien.cx/2025/08/25/simulation-results-of-distributed-fair-assignment-and-rebalancing-in-mobility%e2%80%91on%e2%80%91demand-2/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
