This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
Table of Links
Brief of Homomorphic Polynomial Public Key Cryptography and 4.1 DPPK
Conclusion, References, Acknowledgements, and Author contributions statement
5 HPPK Digital Signature Scheme

\ which reveals the unitary and reversible relation
\

\ Indeed, this encryption operator serves as a distinctive permutation operator or a quantum permutation gate that can be implemented in a native quantum computing system[35, 36]. Furthermore, it adheres to the principles of non-commutativity, i.e.
\

\ The non-commutativity is very important for us to reuse it multiple times to encrypt the entire coefficients of a product polynomial without reducing its security[37], unlike the case of One-Time-Pad encryption with XOR because XOR operator is commutable.
5.1 HPPK DS Algorithm
\

\
\
\

\
\
\

5.2 Signing
The signing algorithm is very straightforward in HPPK DS:
\
\

\ \ \ Following this, the signer appends the signature sig = {F,H} to the message, potentially including the public key if the recipient does not possess it. Upon receiving the message, the recipient can verify the signature using the public key of the HPPK DS. In scenarios where the hash code of the message exceeds the bit length of the finite field Fp, segmentation becomes necessary. Each segment is aligned with Fp, and a signature is independently generated for each segment. Subsequently, the segmented parts are concatenated to form the message’s signature.
\ To prevent signature verification failure, it is advisable to conduct verification, as outlined in subsection 5.3. In the event of verification failure, it is recommended to randomly select a new α ∈ Fp and reevaluate F and H.
5.3 Verify
The signature verification consists of two stages: evaluating signature embedded coefficients and comparing polynomial values at the variable value x. The procedure is as follows
\
\
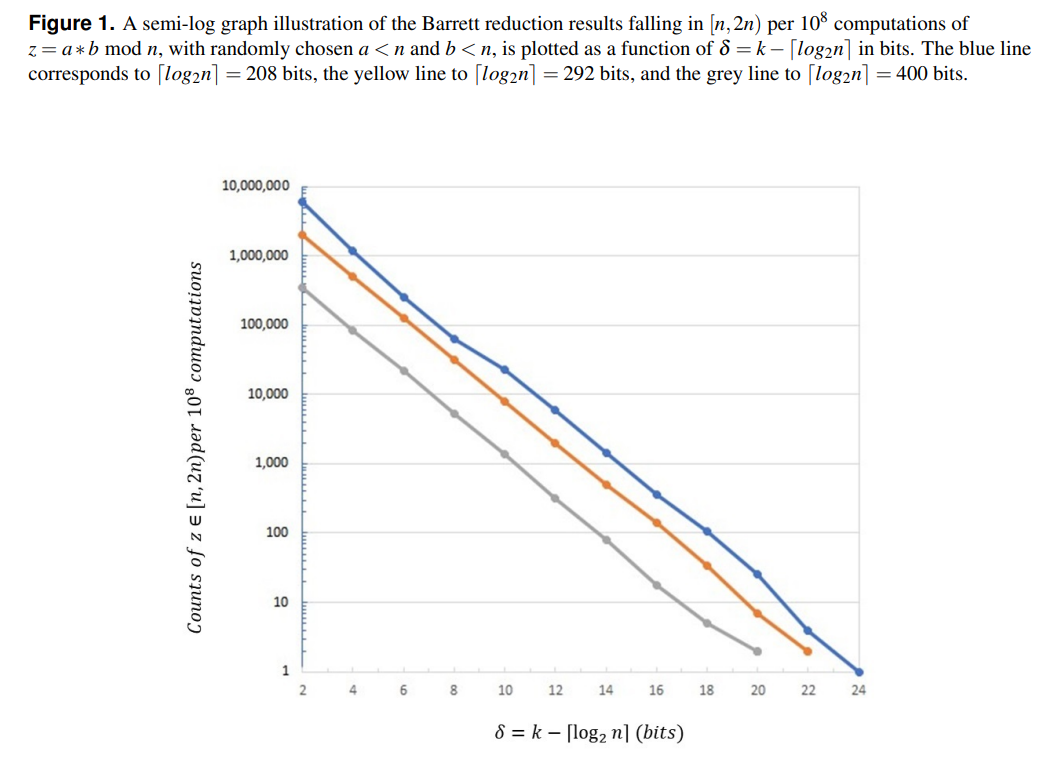
5.4 A Variant of the Barrett Reduction Algorithm
\

5.5 A Toy Example
5.5.1 Key Pair Generation
\
\

\
\
\
\
\
\

\ \ Private Key:
\
\
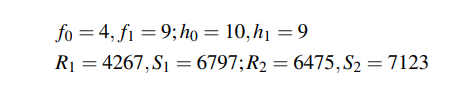
\ \ Public Key: For simplification, we choose β = 1 to evaluate all public key elements.
\
\

\ \ 5.5.2 Signing
\ Assume that the hashed value of a message M is x = 9. Here are steps to generate the signature:
\
\

\ \ 5.5.3 Verify
\
\

\ \ So we obtain the verification polynomials
\
\

\ \ \
:::info Authors:
(1) Randy Kuang, Quantropi Inc., Ottawa, K1Z 8P9, Canada (randy.kuang@quantropi.com);
(2) Maria Perepechaenko, Quantropi Inc., Ottawa, K1Z 8P9, Canada;
(3) Mahmoud Sayed, Systems and Computer Engineering, Carleton University, Ottawa, K1S 5B6, Canada;
(4) Dafu Lou, Quantropi Inc., Ottawa, K1Z 8P9, Canada.
:::
:::info This paper is available on arxiv under ATTRIBUTION-NONCOMMERCIAL-SHAREALIKE 4.0 INTERNATIONAL license.
:::
\
This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
EScholar: Electronic Academic Papers for Scholars | Sciencx (2025-09-23T03:03:05+00:00) A Beginner’s Guide to the HPPK Digital Signature Scheme. Retrieved from https://www.scien.cx/2025/09/23/a-beginners-guide-to-the-hppk-digital-signature-scheme/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
