This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
Table of Links
\
A: Missing Proofs for Sections 2, 3
\

\
\
\

\
\
\

\
\
\
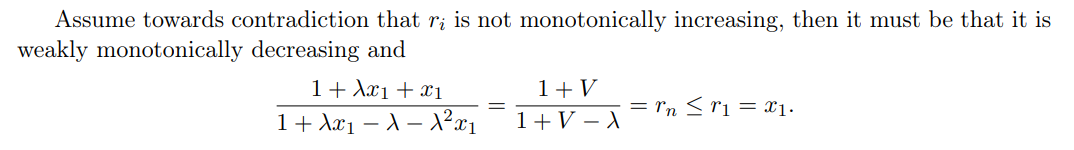
\
\
\

\
\
\

\ \ We now note that a few facts that hold true for any n when x1 ≥ ℓ + ϵ:
\
\

\
\
\

\
\
\

\
\
\

\
\
\
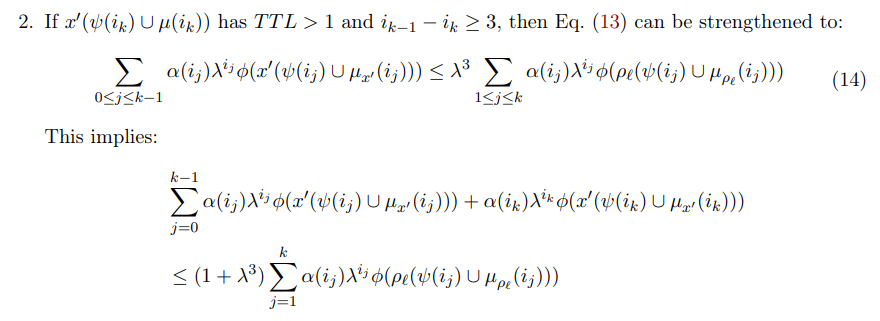
\
\
\

\
\
\

\ \ We separate to several subcases:
\
\

\
\
\

\
\
\

\
\
\

\
\
\

\
\
\

\ \
B Missing Proofs for Section 4

\ We now compare ALG and ADV ’s performance in different steps along the adversary schedule, separating the steps before n and the last two steps.
\ Step i < n.
\ ALG expected performance:
\
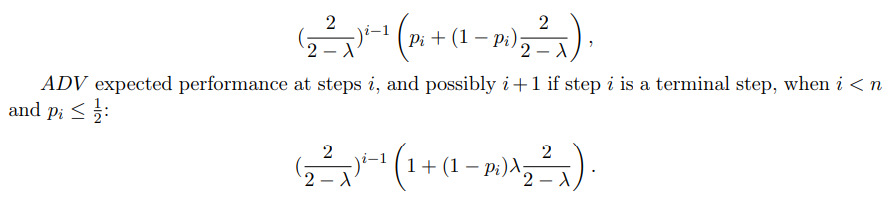
\ Notice that this amortization of considering the i + 1 is only relevant for ADV, as ALG in such case necessarily has no transactions remaining to choose from at step i + 1.
\
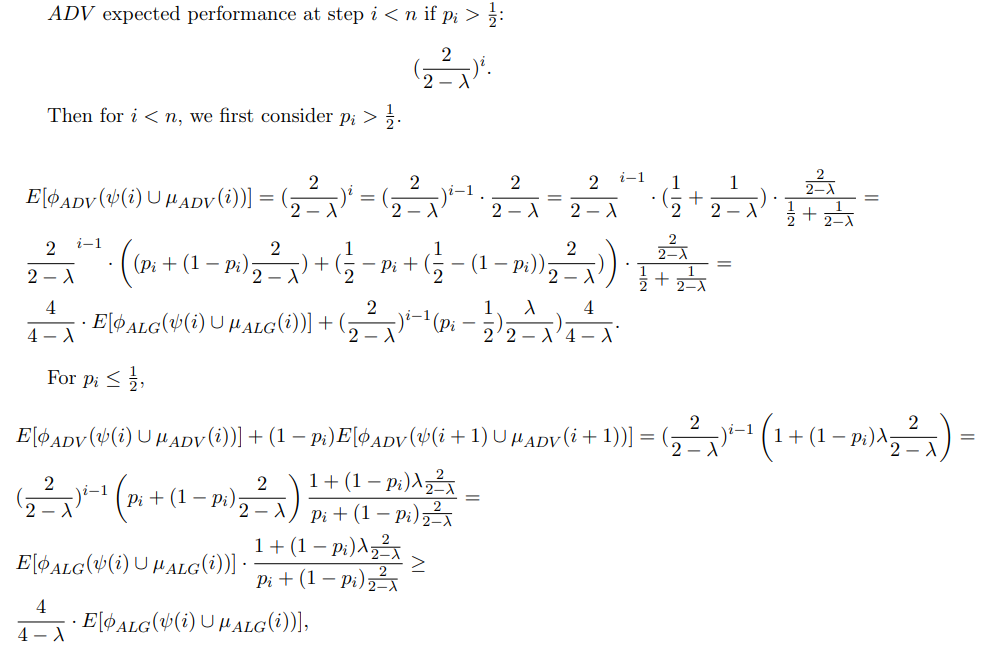
\ where the last transition is since for any 0 ≤ λ ≤ 1, the expression
\
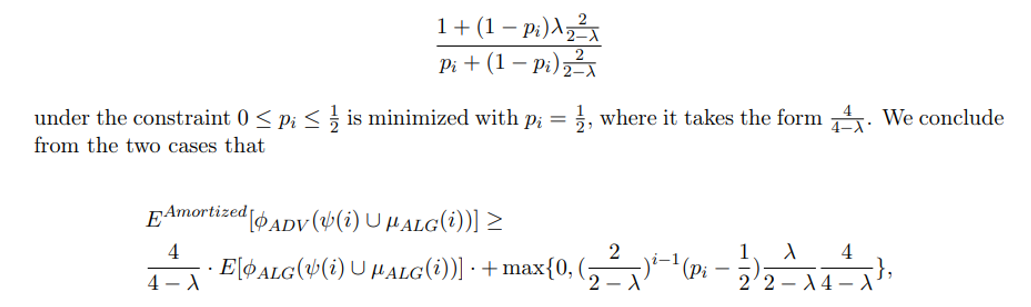
\ We now move on to analyze steps n, n + 1.
\ ALG expected performance at step n, n + 1:
\

\ As the base case, consider k = n. Then,
\
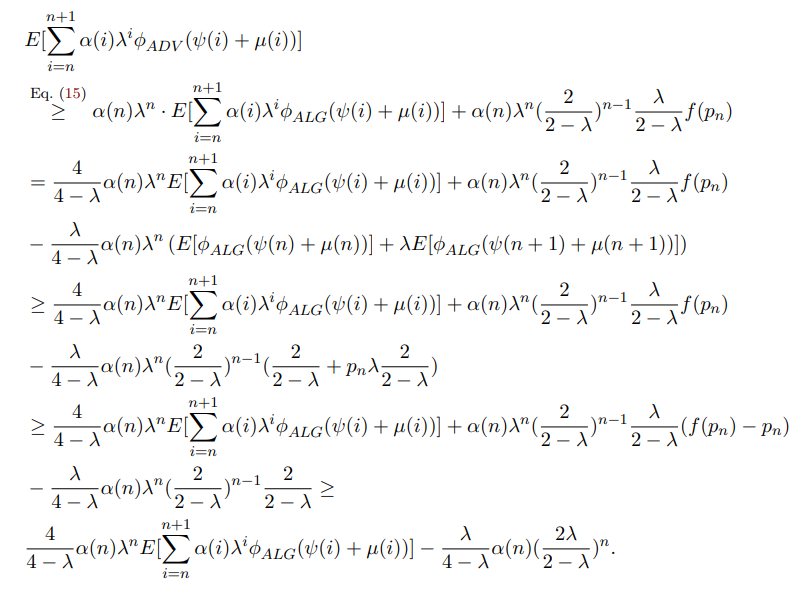
\ For the inductive step,
\
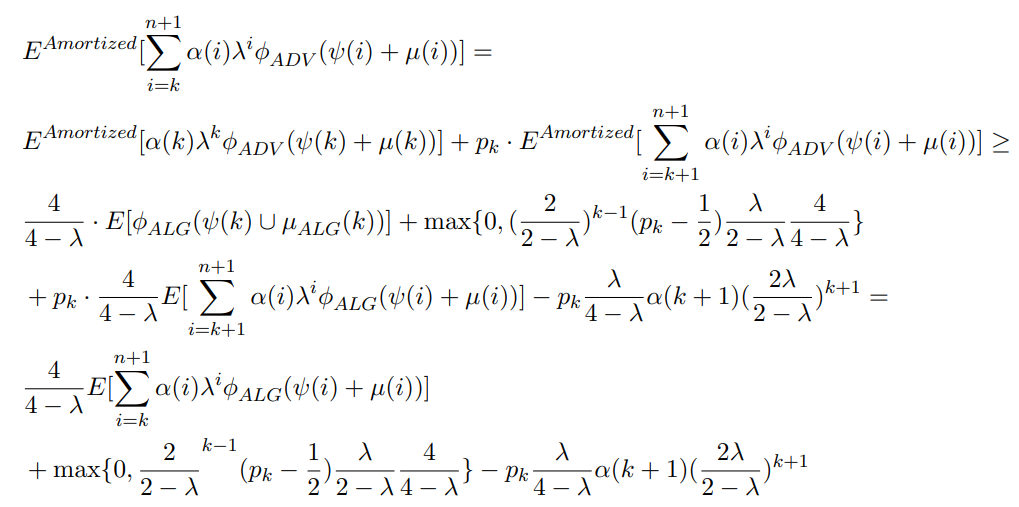
\ We thus need to show that
\
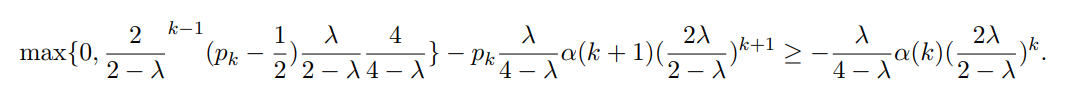
\
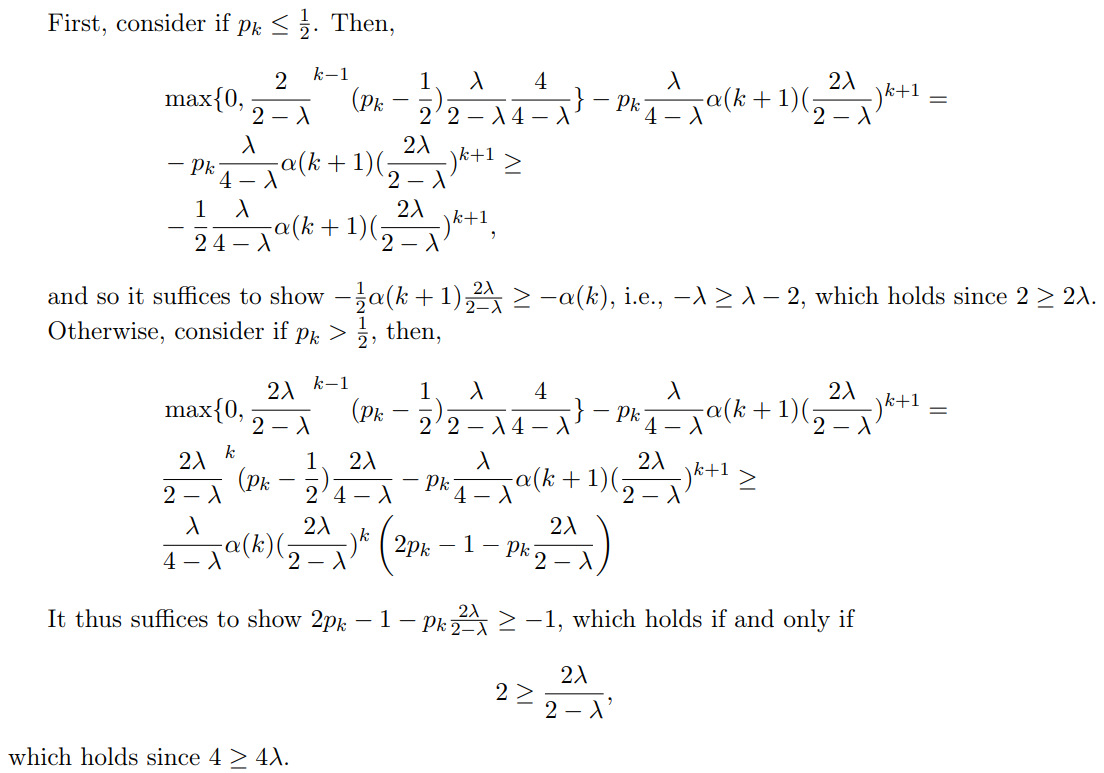
\
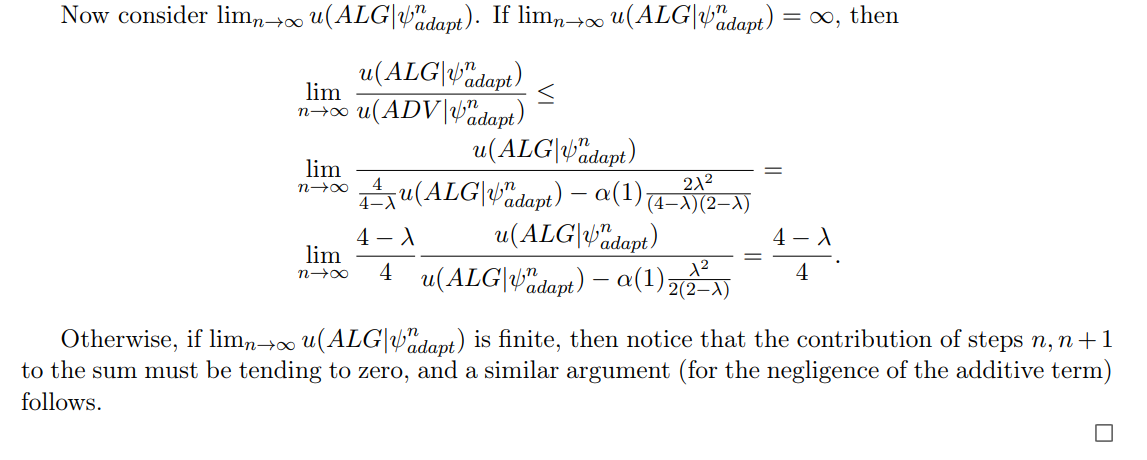
\

\

\ With this potential function, we can thus write at step i,
\
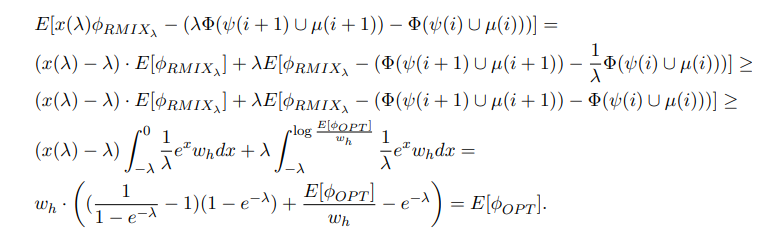
\
C Glossary
A summary of all symbols and acronyms used in the paper.
C.1 Symbols
ψ Transaction schedule function.
\ x Allocation function.
\ B Predefined maximal block-size, in bytes.
\ λ Miner discount factor.
\ ϕ Transaction fee of some transaction, in tokens.
\ T Miner planning horizon.
\ ℓ Immediacy ratio for our non-myopic allocation rule.
\ µ TTL of past transactions.
\ α Miner’s relative mining power, as a fraction. u Miner revenue.
\ t TTL of a transaction.
\ tx A transaction.
C.2 Acronyms
mempool memory pool
\ PoS Proof-of-Stake
\ PoW Proof-of-Work
\ QoS quality of service
\ TFM transaction fee mechanism
\ TTL time to live
\ \
:::info Authors:
(1) Yotam Gafni, Weizmann Institute (yotam.gafni@gmail.com);
(2) Aviv Yaish, The Hebrew University, Jerusalem (aviv.yaish@mail.huji.ac.il).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
[2] The argument of [CCFJST06] is done by showing conditions that hold for any fixed x ∈ [−1, 0], and so they hold for any fixed x ∈ [−λ, 0] as well.
This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
EScholar: Electronic Academic Papers for Scholars | Sciencx (2025-10-14T08:00:16+00:00) The Math Behind Blockchain Scheduling and Transaction Fee Mechanisms. Retrieved from https://www.scien.cx/2025/10/14/the-math-behind-blockchain-scheduling-and-transaction-fee-mechanisms/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
