This content originally appeared on HackerNoon and was authored by Hausdorff
Table of Links
Algorithm
Theoretical Analysis
-
5.1 WormHole𝐸, WormHole𝐻 and BiBFS
4 THEORETICAL ANALYSIS
It is a relatively standard observation that many social networks exhibit, at least approximately, a power-law degree distribution (see, e.g., [9] and the many references within). The Chung-Lu model [41] is a commonly studied random graph model which admits such degree distribution.
\ In this section we provide a proof-of-concept for the correctness of WormHole on Chung-Lu random graphs, aiming to explain the good performance in practice through the study of a popular theoretical model. We sometimes only include proof sketches instead of full proofs, in the interest of saving space.
4.1 Preliminaries

\ Theorem 4.1 (Theorem 4 in [16]). Suppose a power law random graph with exponent 2<𝛽 <3, average degree 𝑑 strictly greater than 1, and maximum degree 𝑑𝑚𝑎𝑥 > log𝑛/log log𝑛. Then almost surely the diameter is Θ(log𝑛), the diameter of the CCL core is 𝑂(loglog𝑛) and almost all vertices are within distance𝑂(loglog𝑛) to CCL.
\ **Claim 4.2 (**Fact 2 in [15]). With probability at least 1−1/𝑛, for all vertices𝑣 ∈𝑉 such that𝑤(𝑣) ≥10logn
\
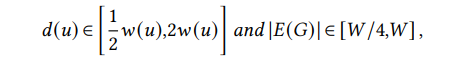
\ and for all vertices with𝑤(𝑣) ≤10log𝑛, 𝑑 (𝑣) ≤20log𝑛.
\
4.2 Sublinearity of Inner Ring
\

\
\
\

\
\
\

\ \ \
:::info Authors:
(1) Talya Eden, Bar-Ilan University (talyaa01@gmail.com);
(2) Omri Ben-Eliezer, MIT (omrib@mit.edu);
(3) C. Seshadhri, UC Santa Cruz (sesh@ucsc.edu).
:::
:::info This paper is available on arxiv under CC BY 4.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by Hausdorff
Hausdorff | Sciencx (2025-10-16T11:00:08+00:00) Understanding Power-Law Degree Distributions in Random Graphs. Retrieved from https://www.scien.cx/2025/10/16/understanding-power-law-degree-distributions-in-random-graphs/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
