This content originally appeared on HackerNoon and was authored by Hyperbole
Table of Links
Low Rank Adaptation
Sparse Spectral Training
4.1 Preliminaries and 4.2 Gradient Update of U, VT with Σ
4.3 Why SVD Initialization is Important
4.4 SST Balances Exploitation and Exploration
4.5 Memory-Efficient Implementation for SST and 4.6 Sparsity of SST
Supplementary Information
A. Algorithm of Sparse Spectral Training
B. Proof of Gradient of Sparse Spectral Layer
C. Proof of Decomposition of Gradient of Weight
D. Proof of Advantage of Enhanced Gradient over Default Gradient
E. Proof of Zero Distortion with SVD Initialization
H. Evaluating SST and GaLore: Complementary Approaches to Memory Efficiency
5 Experiments
To validate our Sparse Spectral Training (SST) approach, we conducted experiments on both Euclidean and hyperbolic neural networks, demonstrating the generalization of SST across various neural network architectures and embedding geometries.
\ We compared SST with full-rank training, LoRA, and ReLoRA*. The key distinctions between ReLoRA* and ReLoRA [5] is that ReLoRA includes a full-rank training as "warm start", making it not an end-to-end memory-efficient method. Moreover, ReLoRA* resets all optimizer states for low-rank parameters, unlike ReLoRA, which resets 99%.
\ For our experiments, all linear layers in the baseline models were modified to their low-rank counterparts. Hyperparameters and implementation details are provided in Appendix F.
\ Further comparisons of SST with the contemporaneous work GaLore [16] are elaborated in Appendix H, highlighting SST’s superior performance in low-rank configurations. Ablation studies are documented in Appendix I.
5.1 Machine Translation
We employ the vanilla transformer [10] as the Euclidean transformer and HyboNet [12] as the hyperbolic transformer. Our experiments include three widely-used machine translation datasets: IWSLT’14 English-to-German [33], IWSLT’17 German-to-English [34], and Multi30K German-toEnglish [35]. For IWSLT’14, the hyperparameters are aligned with those from HyboNet.
\ Table 1 presents BLEU scores for IWSLT’14 across various dimensions and ranks (r). The results confirm that SST consistently outperforms other low-rank methods. Notably, some BLEU scores for the hyperbolic transformer are zero, due to the training process encountering NaN losses, whereas SST maintains stability throughout.
\
\
\ \ Previous hyperbolic neural network articles have predominantly focused on low-dimensional configurations [25, 36, 37]. A key characteristic of hyperbolic space is its exponential growth in volume with distance from a reference point, which is significantly more rapid than the polynomial growth seen in Euclidean space [38]. This expansive nature makes hyperbolic spaces particularly prone to overfitting as dimensionality increases. By imposing constraints on the parameter search space of hyperbolic neural networks, SST prevents the overfitting typically associated with such high-dimensional settings. This spectral sparse constraint enhances the stability and robustness of our models, ensuring consistent performance during training.
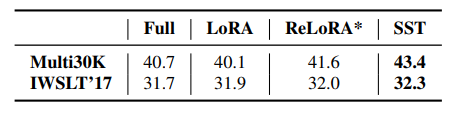
\ Further comparative results on the Multi30K and IWSLT’17 datasets using the standard dimensions for vanilla Euclidean transformers are documented in Table 2. Here, SST not only surpasses other low-rank methods but also demonstrates superior performance compared to full-rank training.
\
:::info Authors:
(1) Jialin Zhao, Center for Complex Network Intelligence (CCNI), Tsinghua Laboratory of Brain and Intelligence (THBI) and Department of Computer Science;
(2) Yingtao Zhang, Center for Complex Network Intelligence (CCNI), Tsinghua Laboratory of Brain and Intelligence (THBI) and Department of Computer Science;
(3) Xinghang Li, Department of Computer Science;
(4) Huaping Liu, Department of Computer Science;
(5) Carlo Vittorio Cannistraci, Center for Complex Network Intelligence (CCNI), Tsinghua Laboratory of Brain and Intelligence (THBI), Department of Computer Science, and Department of Biomedical Engineering Tsinghua University, Beijing, China.
:::
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\
This content originally appeared on HackerNoon and was authored by Hyperbole
Hyperbole | Sciencx (2025-10-29T11:10:19+00:00) Generalizing Sparse Spectral Training Across Euclidean and Hyperbolic Architectures. Retrieved from https://www.scien.cx/2025/10/29/generalizing-sparse-spectral-training-across-euclidean-and-hyperbolic-architectures/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
