This content originally appeared on HackerNoon and was authored by Probabilistic
:::info Authors:
(1) Malte Luttermann[0009 −0005 −8591 −6839], Institute of Information Systems, University of Lubeck, Germany and German Research Center for Artificial Intelligence (DFKI), Lubeck, Germany (luttermann@ifis.uni-luebeck.de);
(2) Ralf Moller[0000 −0002 −1174 −3323], Institute of Information Systems, University of Lubeck, Germany and German Research Center for Artificial Intelligence (DFKI), Lubeck, Germany (moeller@ifis.uni-luebeck.de);
(3) Marcel Gehrke[0000 −0001 −9056 −7673], Institute of Information Systems, University of Lubeck, Germany (gehrke@ifis.uni-luebeck.de).
:::
Table of Links
\ Abstract. Lifting exploits symmetries in probabilistic graphical models by using a representative for indistinguishable objects, allowing to carry out query answering more efficiently while maintaining exact answers. In this paper, we investigate how lifting enables us to perform probabilistic inference for factor graphs containing factors whose potentials are unknown. We introduce the Lifting Factor Graphs with Some Unknown Factors (LIFAGU) algorithm to identify symmetric subgraphs in a factor graph containing unknown factors, thereby enabling the transfer of known potentials to unknown potentials to ensure a well-defined semantics and allow for (lifted) probabilistic inference.
\
1 Introduction
To perform inference in a probabilistic graphical model, all potentials of every factor are required to be known to ensure a well-defined semantics of the model. However, in practice, scenarios arise in which not all factors are known. For example, consider a database of a hospital containing patient data and assume a new patient arrives and we want to include them into an existing probabilistic graphical model such as a factor graph (FG). Clearly, not all attributes of the database are measured for every new patient, i.e., there are some values missing, resulting in an FG with unknown factors and ill-defined semantics when including a new patient in an existing FG. Therefore, we aim to add new patients to an existing group of indistinguishable patients to treat them equally in the FG, thereby allowing for the imputation of missing values under the assumption that there exists such a group for which all values are known. In particular, we study the problem of constructing a lifted representation having well-defined semantics for an FG containing unknown factors—that is, factors whose mappings from input to output are unknown. In probabilistic inference, lifting exploits symmetries in a probabilistic graphical model, allowing to carry out query answering more efficiently while maintaining exact answers [12]. The main idea is to use a representative of indistinguishable individuals for computations. By lifting the probabilistic graphical model, we ensure a well-defined semantics of the model and allow for tractable probabilistic inference with respect to domain sizes.
\ Previous work on constructing a lifted representation builds on the WeisfeilerLeman algorithm [15] which incorporates a colour passing procedure to detect symmetries in a graph, e.g. to test for graph isomorphism. To construct a lifted representation for a given FG where all factors are known, the colour passing (CP) algorithm (originally named “CompressFactorGraph”) [1,7] is commonly used. Having obtained a lifted representation, algorithms performing lifted inference can be applied. A widely used algorithm for lifted inference is the lifted variable elimination algorithm, first introduced by Poole [13] and afterwards refined by many researchers to reach its current form [3,4,8,11,14]. Another prominent algorithm for lifted inference is the lifted junction tree algorithm [2], which is designed to handle sets of queries instead of single queries.
\ To encounter the problem of constructing a lifted representation for an FG containing unknown factors, we introduce the Lifting Factor Graphs with Some Unknown Factors (LIFAGU) algorithm, which is a generalisation of the CP algorithm. LIFAGU is able to handle arbitrary FGs, regardless of whether all factors are known or not. By detecting symmetries in an FG containing unknown factors, LIFAGU generates the possibility to transfer the potentials of known factors to unknown factors to eliminate unknown factors from an FG. We show that, under the assumption that for every unknown factor there is at least one known factor having a symmetric surrounding graph structure to it, all unknown potentials in an FG can be replaced by known potentials. Thereby, LIFAGU ensures a well-defined semantics of the model and allows for lifted probabilistic inference.
\ The remaining part of this paper is structured as follows. Section 2 introduces necessary background information and notations. We first briefly recapitulate FGs, afterwards define parameterised factor graphs (PFGs), and then describe the CP algorithm as a foundation for LIFAGU. Afterwards, in Section 3, we introduce LIFAGU as an algorithm to obtain a lifted representation for an FG that possibly contains unknown factors. We present the results of our empirical evaluation in Section 4 before we conclude in Section 5.
\
2 Preliminaries
In this section, we begin by defining FGs as a propositional representation for a joint probability distribution between random variables (randvars) and then introduce PFGs, which combine probabilistic models and first-order logic. Thereafter, we describe the well-known CP algorithm to lift a propositional model, i.e., to transform an FG into a PFG with equivalent semantics.
\
2.1 Factor Graphs and Parameterised Factor Graphs
\

\
![Fig. 1: An FG for an epidemic example [6] with two individuals alice and bob. The input-output pairs of the factors are omitted for simplification.](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-av032mo.png)
\ Clearly, the size of the FG increases with an increasing number of individuals even though it is not necessary to distinguish between individuals because there are symmetries in the model (the factor f1 occurs two times and the factor f2 occurs four times). In other words, the probability of an epidemic does not depend on knowing which specific individuals are being sick, but only on how many individuals are being sick. To exploit such symmetries in a model, PFGs can be used. We define PFGs, first introduced by Poole [13], based on the definitions given by Gehrke et al. [5]. PFGs combine first-order logic with probabilistic models, using logical variables (logvars) as parameters in randvars to represent sets of indistinguishable randvars, forming parameterised randvars (PRVs).
\

\
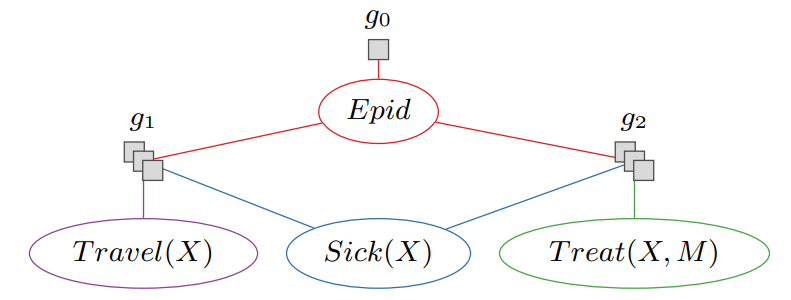
\

\
2.2 The Colour Passing Algorithm
The CP algorithm [1,7] constructs a lifted representation for an FG where all factors are known. As LIFAGU generalises CP, we briefly recap how the CP algorithm works. The idea is to find symmetries in an FG based on potentials of factors, ranges and evidence of randvars, as well as on the graph structure. Each randvar is assigned a colour depending on its range and evidence, meaning that randvars with identical ranges and identical evidence are assigned the
\
\
![Fig. 3: The colour passing procedure of the CP algorithm on an exemplary input FG containing three Boolean randvars without evidence and two factors with identical potentials. The example has been introduced by Ahmadi et al. [1].](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-n2133l8.png)
\ \ same colour, and each factor is assigned a colour depending on its potentials, i.e., factors with the same potentials get the same colour. The colours are then passed from every randvar to its neighbouring factors and vice versa. Passing colours around is repeated until the groupings of identical colours do not change anymore. In the end, randvars and factors, respectively, are grouped together based on their colour signatures.
\ Figure 3 depicts the procedure of the CP algorithm on a simple FG. The two factors ϕ1 and ϕ2 share identical potentials in this example. As all three randvars are Boolean and there is no evidence available, A, B, and C are assigned the same colour (e.g., green). Furthermore, the potentials of ϕ1 and ϕ2 are identical, so they are assigned the same colour (e.g., purple). The colours are then passed from randvars to factors: ϕ1 receives two times the colour green from A and B and ϕ2 receives two times the colour green from B and C. Afterwards, ϕ1 and ϕ2 are recoloured according to the colours they received from their neighbours. Since both ϕ1 and ϕ2 received the same colours, they are assigned the same colour during recolouring (e.g., purple). The colours are then passed from factors to randvars. During this step, not only the colours are shared but also the position of the randvars in the argument list of the corresponding factor. Thus, A receives a tuple (purple, 1) from ϕ1, B receives (purple, 2) from ϕ1 and (purple, 2) from ϕ2, and C receives (purple, 1) from ϕ2. Building on these new colour signatures, the randvars are recoloured such that A and C receive the same colour while B is assigned a different colour. Iterating the colour passing procedure does not change these groupings and thus we obtain the PFG shown on the right in Fig. 3.
\ When facing a situation with unknown factors being present in an FG, the CP algorithm cannot be applied to construct a lifted representation for the FG. In the upcoming section, we introduce the LIFAGU algorithm which generalises the CP algorithm and is able to handle the presence unknown factors.
\
:::info This paper is available on arxiv under ATTRIBUTION-SHAREALIKE 4.0 INTERNATIONAL license.
:::
\
This content originally appeared on HackerNoon and was authored by Probabilistic
Probabilistic | Sciencx (2025-08-25T20:55:57+00:00) LIFAGU: Lifted Probabilistic Inference in Factor Graphs with Unknown Factors. Retrieved from https://www.scien.cx/2025/08/25/lifagu-lifted-probabilistic-inference-in-factor-graphs-with-unknown-factors-2/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
