This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
Table of Links
III. Secure and Private Source Coding Regions
IV. Gaussian Sources and Channels
III. SECURE AND PRIVATE SOURCE CODING REGIONS
A. Lossy Source Coding
\ The lossy secure and and private source coding region RD is characterized below; see Section V for its proof.
\
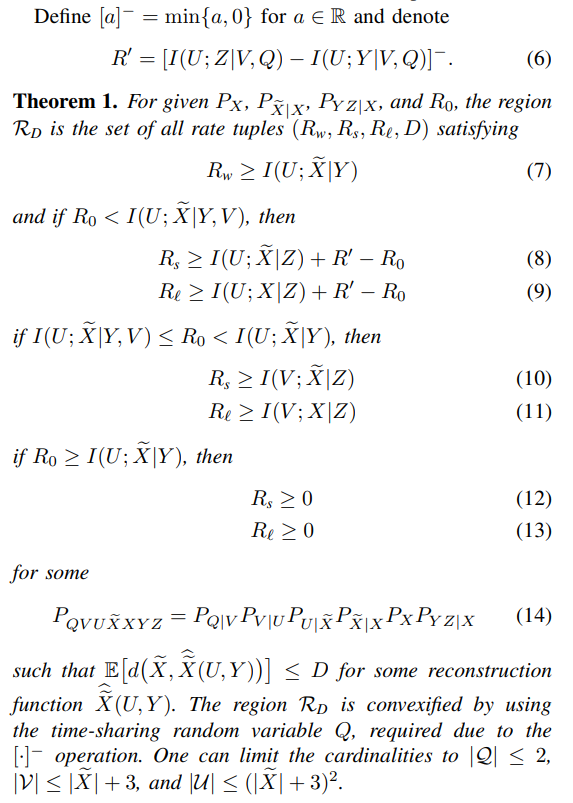
\ We remark that (12) and (13) show that one can simultaneously achieve strong secrecy and strong privacy, i.e., the conditional mutual information terms in (2) and (3), respectively, are negligible, by using a large private key K, which is a result missing in some recent works on secure source coding with private key.
\ B. Lossless Source Coding
\ The lossless secure and and private source coding region R is characterized next; see below for a proof sketch.
\ Denote
\
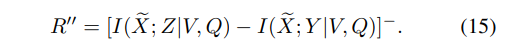
\
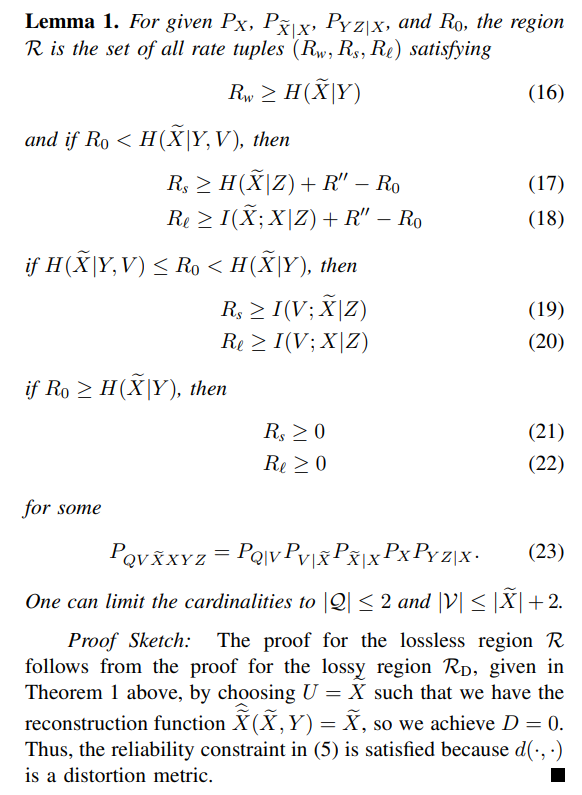
\
IV. GAUSSIAN SOURCES AND CHANNELS

\

\ Suppose the following scalar discrete-time Gaussian source and channel model for the lossy source coding problem depicted in Fig.
\

\ We next take the liberty to use the lossy rate region in Corollary 1, characterized for discrete memoryless channels, for the model in (29)-(31). This is common in the literature since there is a discretization procedure to extend the achievability proof to well-behaved continuous-alphabet random variables and the converse proof applies to arbitrary random variables; see [2, Remark 3.8]. For Gaussian sources and channels, we use differential entropy and eliminate the cardinality bound on the auxiliary random variable. The lossy source coding region for the model in (29)-(31) without a private key is given below.
\

\

\ One can also show that
\
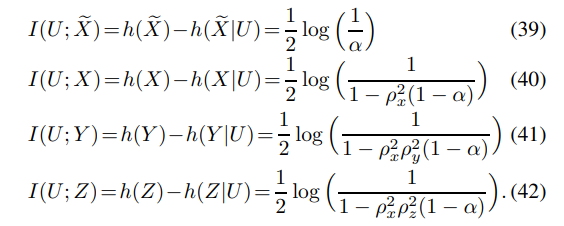
\ Thus, by calculating (25)-(27), the achievability proof follows.
\ For the converse proof, one can first show that
\
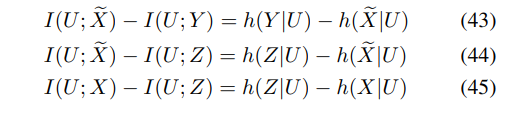
\

\

\ Next, consider
\

\ Combining the distortion constraint given in Corollary 1 with (50) and (51), the converse proof for (35) follows.
\ \
:::info Authors:
(1) Onur Gunlu, Chair of Communications Engineering and Security, University of Siegen and Information Coding Division, Department of Electrical Engineering, Linkoping University (onur.guenlue@uni-siegen.de);
(2) Rafael F. Schaefer, Chair of Communications Engineering and Security, University of Siegen (rafael.schaefer@uni-siegen.de);
(3) Holger Boche, Chair of Theoretical Information Technology, Technical University of Munich, CASA: Cyber Security in the Age of Large-Scale Adversaries Exzellenzcluster, Ruhr-Universitat Bochum, and BMBF Research Hub 6G-Life, Technical University of Munich (boche@tum.de);
(4) H. Vincent Poor, Department of Electrical and Computer Engineering, Princeton University (poor@princeton.edu).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
EScholar: Electronic Academic Papers for Scholars | Sciencx (2025-09-02T20:41:05+00:00) Can Coding Be Both Lossless and Private?. Retrieved from https://www.scien.cx/2025/09/02/can-coding-be-both-lossless-and-private/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
