This content originally appeared on phpied.com and was authored by Stoyan
Previously on "Deep Note via WebAudio":
Nodes
WebAudio makes a heavy use of the concept of nodes. A node is something that does a thing (I know, very helpful), for example makes noise or manipulates sound somehow. Then you connect the various nodes in any way you see fit to produce the desired outcome. In Graph Theory parlance this is like the concept of vertices (nodes) and edges (links). In guitar player parlance this is like a bunch of pedals connected with cables.

Similar for modular synthesizers. In fact, WebAudio nodes seem mostly inspired by synthesizes, where you have oscillators (see part 2.1. of this series) that make sound and other stuff such as like amplifiers (similar to gain which is today's topic), equalizers and such.

Nodes in the examples so far
In the previous installment there was no mention about nodes, but they were still there. Let's look back at the very first example: playing a sound. The audio context destination is one node. The buffer source we created to play a sample was another node. When we connected them like so:
sample.connect(audioContext.destination);
Representing this graphically looks like:
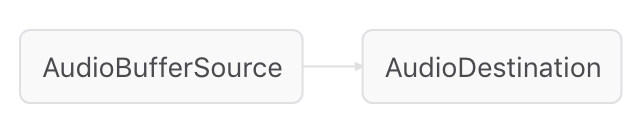
Just like we had something capable of playing a file (maybe an MP3 player) and we plugged a cable from the headphone jack to something capable of producing sound, like headphones or a set of speakers.
Similarly, the previous post was about playing 30 sounds together, so 30 buffer source nodes, all connected to the same destination node. Abbreviated, this visualizes like so:
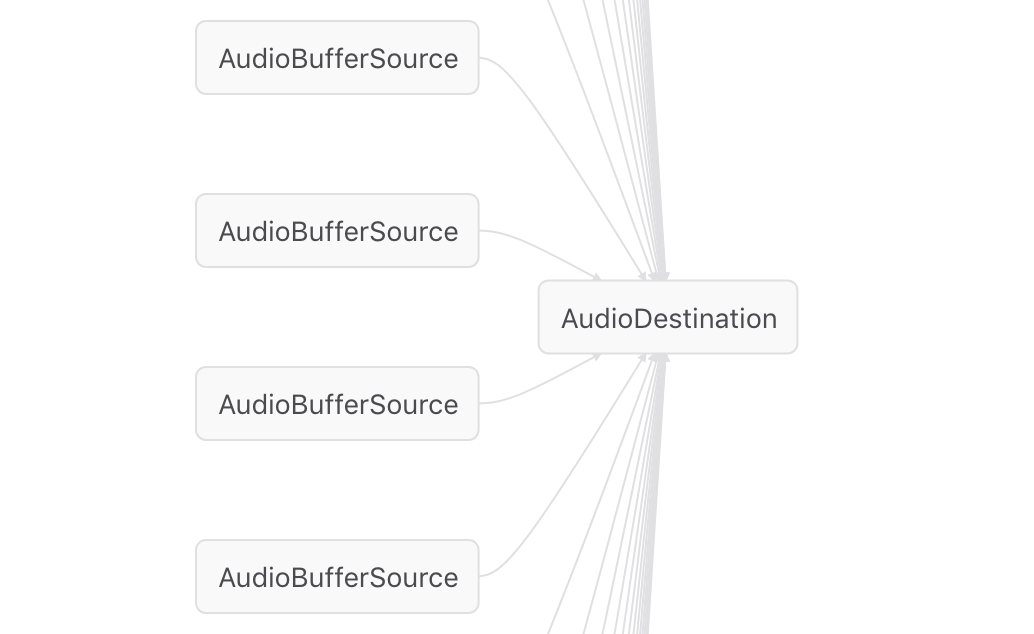
Visualizing nodes
"Nice graphs!", you're probably thinking. I know, I know, I'm that amazing. In this case I just used the built-in WebAudio editor right in Firefox's dev tools. It's really helpful to be able to visualize these connections. Because it happens every once in a while that you do something in web audio (like create a node) and you forget to connect it and then you wonder why on Earth the result doesn't sound like you imagined.
Now for the bad news. This Web Audio editor has been deprecated. Chrome has a Web Audio tab in its devtools but it's not even close. There are two alternatives listed on the Firefox deprecation page, I personally didn't manage to get one of them to work (although it looks very promising), but the other one worked just fine.
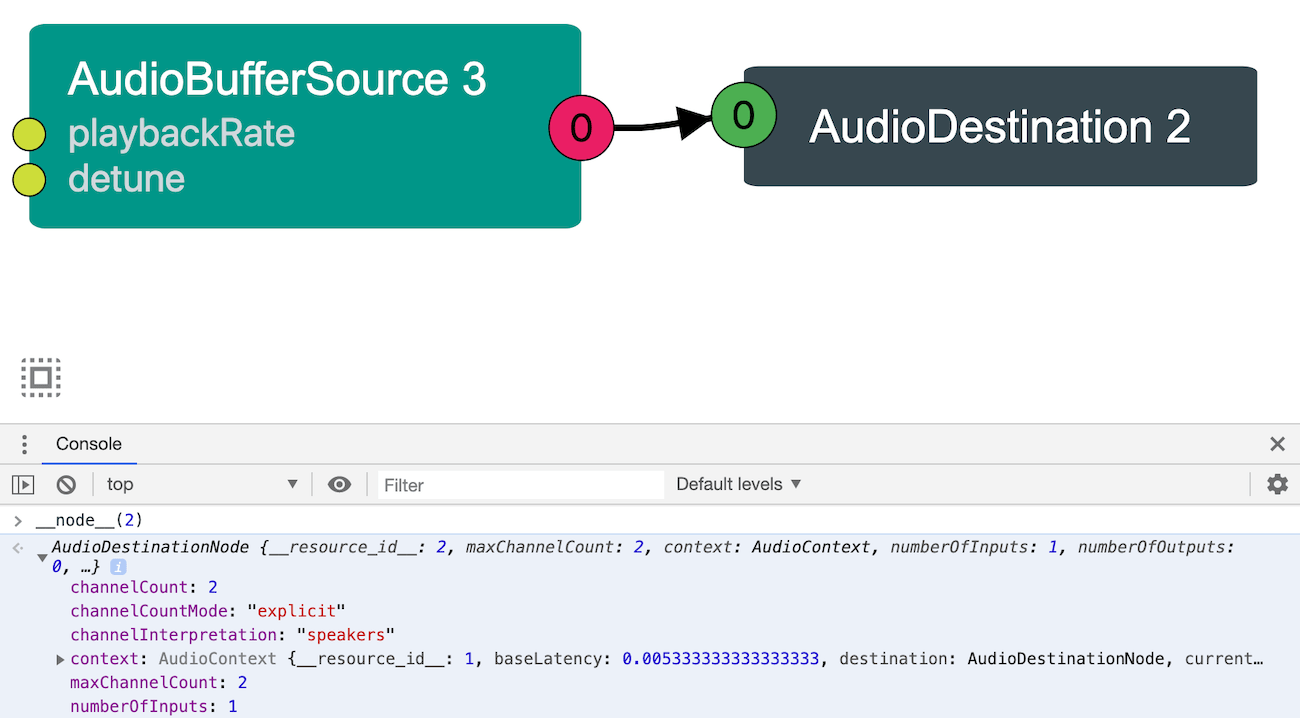
This WebAudio Inspector adds IDs to the nodes (not sure what the logic is as to the actual numbers) and you can even inspect nodes in the console with the __node__() function.
So that's it about nodes, next time - the Gain node!
Photo credits
- Anton Shuvalov (pedalboard)
- Steve Harvey (synth)
This content originally appeared on phpied.com and was authored by Stoyan
Stoyan | Sciencx (2019-11-04T04:00:29+00:00) WebAudio Deep Note, part 5: nodes. Retrieved from https://www.scien.cx/2019/11/04/webaudio-deep-note-part-5-nodes/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
