This content originally appeared on HackerNoon and was authored by Computational Technology for All
Table of Links
4 Members of Deep Π0 1 classes
5. Strong Depth is Negligible

\ Theorem 25. The class of strongly deep sequences is negligible.
\ Proof. For the sake of contradiction, assume there exists a functional Φ such that
\

\ It is clear that q is computable. Moveover, q is a discrete semimeasure, since
\
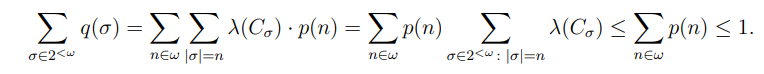
\

\ On the other hand, for almost all n:
\

\ Note, by contrast, that the collection of weakly deep sequences is not negligible. Indeed, as shown by Muchnik et al. [MSU98], no 1-generic sequence is Martin-L¨of random with respect to a computable measure, and thus every 1-generic is weakly deep. Moreover, as shown by Kautz [Kau91], every 2-random sequence computes a 1-generic, and hence the collection of 1-generics is not negligible.
\

\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
:::info Authors:
(1) Laurent Bienvenu;
(2) Christopher P. Porter.
:::
\
This content originally appeared on HackerNoon and was authored by Computational Technology for All
Computational Technology for All | Sciencx (2025-01-17T02:48:00+00:00) Bridging Computational Notions of Depth: Here’s Why Strong Depth is Negligible. Retrieved from https://www.scien.cx/2025/01/17/bridging-computational-notions-of-depth-heres-why-strong-depth-is-negligible/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
