This content originally appeared on HackerNoon and was authored by Labyrinthine
Table of Links
1.1 A Polyethylene-based metamaterial for acoustic control
2 Relaxed micromorphic modelling of finite-size metamaterials
2.1 Tetragonal Symmetry / Shape of elastic tensors (in Voigt notation)
4 New considerations on the relaxed micromorphic parameters
4.2 Consistency of the relaxed micromorphic model with respect to a change in the unit cell’s size
4.3 Relaxed micromorphic cut-offs
6 Fitting of the relaxed micromorphic parameters with curvature (with Curl P)
6.1 Asymptotes and 6.2 Fitting
8 Summary of the obtained results
9 Conclusion and perspectives, Acknowledgements, and References
A Most general 4th order tensor belonging to the tetragonal symmetry class
B Coefficients for the dispersion curves without Curl P
C Coefficients for the dispersion curves with P
D Coefficients for the dispersion curves with P◦

7.1 Asymptotes
Again, the cut-offs are independent on the coefficients with higher order of k and thus they do not change with respect to the two previous cases. For the asymptotes we only consider the terms with the highest order of k available and compute
\
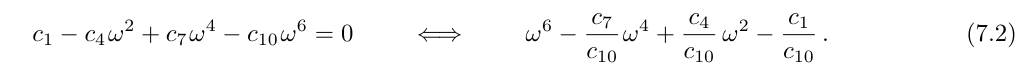
\ We have again three asymptotes (the roots of a third order polynomial) which in general causes the analytical expressions to be impractical rather quickly. However, in this case it is possible to find one root by hand
\

\
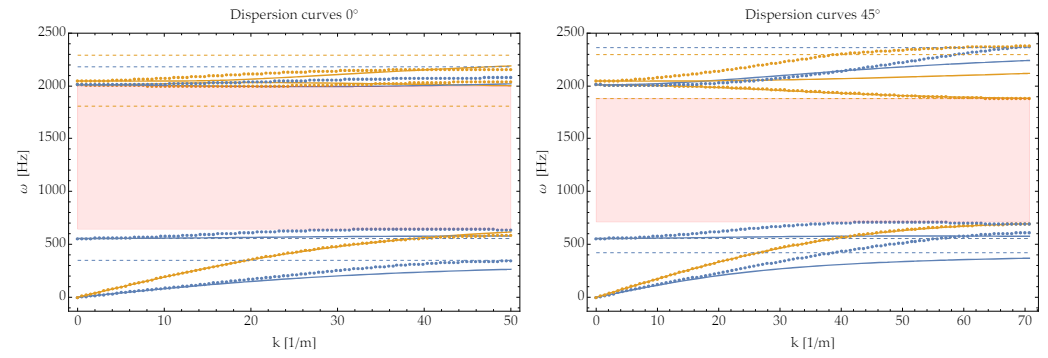
7.2 Fitting
\

7.3 Discussion
\

\
\
\
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
:::info Authors:
(1) Jendrik Voss, Institute for Structural Mechanics and Dynamics, Technical University Dortmund and a Corresponding Author (jendrik.voss@tu-dortmund.de);
(2) Gianluca Rizzi, Institute for Structural Mechanics and Dynamics, Technical University Dortmund;
(3) Patrizio Neff, Chair for Nonlinear Analysis and Modeling, Faculty of Mathematics, University of Duisburg-Essen;
(4) Angela Madeo, Institute for Structural Mechanics and Dynamics, Technical University Dortmund.
:::
\
This content originally appeared on HackerNoon and was authored by Labyrinthine
Labyrinthine | Sciencx (2025-03-23T17:30:50+00:00) The Science Behind Stronger, Smarter Materials. Retrieved from https://www.scien.cx/2025/03/23/the-science-behind-stronger-smarter-materials/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
