This content originally appeared on DEV Community and was authored by Deniss Sudak
In Part 1, we discussed how to match applicants to roles. In this part, we’ll explore how to determine which roles need to be filled to complete the team. Let’s describe this problem through examples.
Let’s start with a simple case. Suppose we have a job that needs two people with “skill-1.” We’ve assigned this role to one person. We still need someone with “skill-1” to complete the team.
Now let’s say we have a job that requires one person with “skill-1” and one person with “skill-2.” We’ve assigned the “skill-1” role to someone who has both “skill-1” and “skill-2.” To complete the team, we obviously need someone with “skill-2,” but actually, someone with “skill-1” will do as well, as we can reassign the current applicant to the “skill-2” role.
As you can imagine, in complex scenarios with multiple roles and applicants with multiple skills, we can reshuffle role assignments in many ways to accommodate a new applicant who helps complete the team.
Here, we’ll discuss how to determine which applicants with which skills could join the team without replacing anyone currently on it.
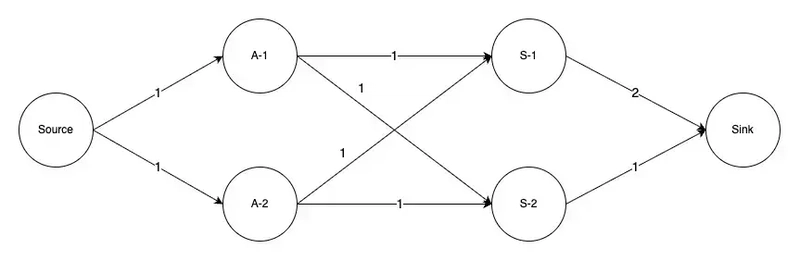
Suppose we have the following roles to fill:
And right now, we have two applicants:
In other words, any applicant is suitable for any role.
Here’s how our problem would look like in a flow network form.
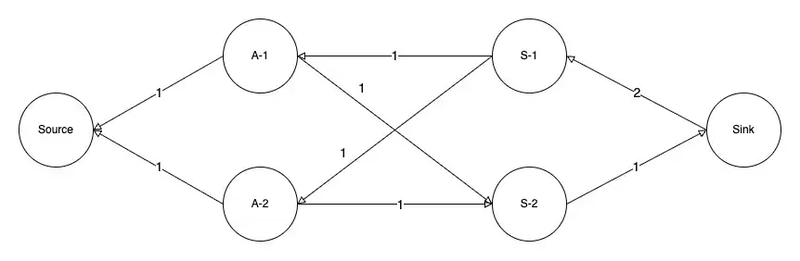
Now, let’s say that after running our matching algorithm, both applicant-1 and applicant-2 are assigned to the “skill-1” role. To do that, I’m running a push-relabel maximum flow algorithm. By the time it terminates, the original network will have been transformed into the following residual graph:
You can think of a residual graph as a network of the remaining (residual) capacity after the flow has been set. For example, since applicant-1 is assigned the “skill-1” role, there is no more flow from A-1 to S-1. However, it’s possible to “undo” this assignment by directing flow from the Sink to S-1 and from S-1 to A-1. From there, excess can flow to S-2 and then to the Sink, thus reassigning applicant-1 to the “skill-2” role.
So how do we determine which applicants with which skills could join the team without replacing anyone already on it?
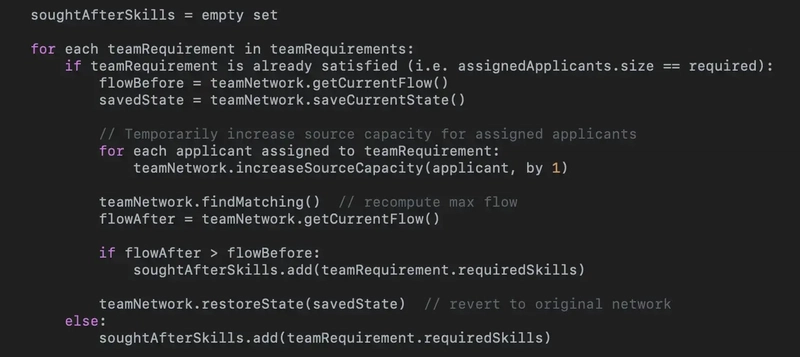
If a team requirement needs more members than are currently assigned, then clearly we need applicants with those skills.
If a team requirement is already satisfied — that is, it has the number of team members it requires (like S-1 in our example) — then we need to check whether at least one of those team members could be reassigned to another role. We do that in the following way:
We add 1 to the capacity of the arc that emanates from the Source and ends at each node corresponding to team members linked to the team requirement in question. If that increases the flow, then at least one of those team members found another role (without displacing anyone), and so we can say that we need another applicant with those skills.
This is like cloning applicants already assigned to a role and then checking if at least one of them can take on a different role without kicking anyone out.
Try it yourself
You can experiment with this algorithm using the following repo:
👉 https://github.com/denissudak/applicant-job-matching
I hope you’ll find it useful.
This content originally appeared on DEV Community and was authored by Deniss Sudak
Deniss Sudak | Sciencx (2025-06-09T01:48:43+00:00) Applying matching algorithms to real allocation problems. Part 2. Retrieved from https://www.scien.cx/2025/06/09/applying-matching-algorithms-to-real-allocation-problems-part-2/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.