This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
Table of Links
IDEAL-TFRM: Impossibility of Achieving Strictly Positive Redistribution Index
R-TFRM: A TFRM Robust to Miner Manipulation
6.1 R-TFRM: Analyzing Impact of Miner Manipulation on Rebate and Miner Revenue
A. Proofs for Results from Section 4 and 5
B. Proofs for Results from Section 6
C. Proofs for Results from Section 7
\
A PROOFS FOR RESULTS FROM SECTION 4 AND 5
A.1 Proof of Theorem 2
Theorem (Ideal-TFRM Impossibility). If𝑟 ★ is an anonymous rebate function that satisfies Theorem 1, no Ideal-TFRM can guarantee a non-zero redistribution index (RI) in the worst case.
\

A.2 Proof of Theorem 3

B PROOFS FOR RESULTS FROM SECTION 6
B.1 Proof of Claim 1
\

\
B.2 Proof of Claim 2
\

\
B.3 Proof of Claim 3
\

\
B.4 Proof of Claim 4
\

\
B.5 Proof of Theorem 4
Theorem*. For any𝑛 and 𝑘 such that𝑛 ≥ 𝑘+2, the R-TFRMmechanism is unique. The fraction redistributed to the top-k users in the worst-case is given by:*
\
\

\
B.6 Proof of Theorem 5
\

\
C PROOFS FOR RESULTS FROM SECTION 7
C.1 Proof of Theorem 6
\

\
C.2 Proof of Theorem 7
\
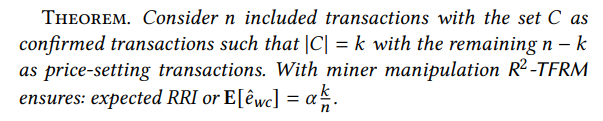
\ \ Proof. Similar to Theorem 5, the fraction of redistribution remains constant. For every true user (not fake), the 𝛼𝑘/𝑛 fraction of the payment is returned back as the rebate in expectation.
\
:::info Authors:
(1) Sankarshan Damle, IIIT, Hyderabad, Hyderbad, India (sankarshan.damle@research.iiit.ac.in);
(2) Manisha Padala, IISc, Bangalore, Bangalore, India (manishap@iisc.ac.in);
(3) Sujit Gujar, IIIT, Hyderabad, Hyderbad, India (sujit.gujar@iiit.ac.in).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by EScholar: Electronic Academic Papers for Scholars
EScholar: Electronic Academic Papers for Scholars | Sciencx (2025-07-01T06:00:08+00:00) Mathematical Proofs for Truthful Rebate Mechanisms (TFRM). Retrieved from https://www.scien.cx/2025/07/01/mathematical-proofs-for-truthful-rebate-mechanisms-tfrm/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.

