This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Table of Links
Translating To Sequent Calculus
Evaluation Within a Context
Insights
5.1 Evaluation Contexts are First Class
5.3 Let-Bindings are Dual to Control Operators
5.4 The Case-of-Case Transformation
5.5 Direct and Indirect Consumers
Conclusion, Data Availability Statement, and Acknowledgments
A. The Relationship to the Sequent Calculus
C. Operational Semantics of label/goto
2.2 Let Bindings
Let-bindings are important since we can use them to eliminate duplication and make code more readable. In this section we introduce let-bindings to Fun for an additional reason: they allow us to introduce the second construct which gives the 𝜆𝜇𝜇˜-calculus its name: 𝜇˜-abstractions.
\

\ The let-bindings in Fun are standard and are evaluated by substituting the value 𝔱 for the variable 𝑥 in the body which is a term. The analogue of a let-binding in Fun is a 𝜇˜-binding in Core which also binds a variable, with the difference that the body of a 𝜇˜-binding is a statement. It can easily be seen that 𝜇˜-bindings are the precise dual of 𝜇-bindings that we have already introduced.
\ With both 𝜇- and 𝜇˜-bindings in Core we have to face a potential problem, namely statements of the form ⟨𝜇𝛼.𝑠1 | 𝜇𝑥.𝑠 ˜ 2⟩. Such a statement is called a critical pair since it can potentially be reduced to both 𝑠1 [𝜇𝑥.𝑠 ˜ 2/𝛼] and 𝑠2 [𝜇𝛼.𝑠1/𝑥] which can be a source of non-confluence. A closer inspection of the rules shows that we avoid this pitfall and always evaluate the statement to 𝑠1 [𝜇𝑥.𝑠 ˜ 2/𝛼]. We do not allow to reduce the statement to 𝑠2 [𝜇𝛼.𝑠1/𝑥] since only values 𝔭 can be substituted for variables, and 𝜇𝛼.𝑠1 is not a value. This restriction precisely mirrors the restriction on the evaluation of let-bindings in Fun. In other words, we use call-by-value evaluation order. We will address the critical pair and how it relates to different evaluation orders again in Section 5.6.
\

\ We can observe that the arithmetic expression 2 ∗ 2 has been evaluated only once, which is precisely what we expect from call-by-value.
2.3 Top-level Definitions
We introduce recursive top-level definitions to Fun and Core for two reasons. They allow us to write more interesting examples and they illustrate a difference in how recursive calls are handled. The extension is specified in Definition 2.4.
\
\

\ \ Top-level definitions should not be confused with first-class functions which will be introduced later, since they cannot be passed as an argument or returned as a result. They are a part of a program that consists of a list of such top-level definitions. The top-level definitions in Fun curiously also take covariables as arguments even though the language does not contain consumers; you can ignore that for now. If you remember the example from the introduction, then you might recall that we use them for passing labels, but we will only formally introduce that construct in Section 2.6.
\ We evaluate the call of a top-level definition by looking up the body in the program and substituting the arguments of the call for the parameters in the body of the definition. The body of a top-level definition is a term in Fun and a statement in Core. This difference explains why we have to add an additional parameter 𝛼 to every top-level definition when we translate it; this parameter 𝛼 also corresponds to the additional continuation argument when we ordinarily translate a function into continuation-passing style. We could also have specified that the body of a top-level definition in Core should be a producer. We don’t do that because when we eventually translate Core to machine code we want every top-level definition to become the target of a jump with arguments without building up a function call stack. The following example shows how this works:
\ Example 2.3. Using a top-level definition, we can represent the factorial function in Core.
\
\
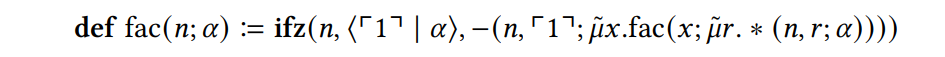
\ \ For the argument ⌜1⌝ this evaluates in the following way:
\
\

\ \ At the point (∗) of the evaluation we can now see how the recursive call is evaluated. In Fun this recursive call would have the form 1 ∗ fac(0) and require a function stack, but in Core we can jump to the definition of fac with the consumer 𝜇𝑟 . ˜ ∗ (⌜1⌝, 𝑟; ⋆) as an additional argument which contains the information that the result of the recursive call should be bound to the variable 𝑟 and then multiplied with ⌜1⌝. Note again that this consumer argument corresponds to a continuation in continuation-passing style (in that sense it might be viewed as a reified stack) and so the basic techniques used in CPS-based intermediate representations and compilers can be applied for its implementation.
\
:::info Authors:
(1) David Binder, University of Tübingen, Germany;
(2) Marco Tzschentke, University of Tübingen, Germany;
(3) Marius Muller, University of Tübingen, Germany;
(4) Klaus Ostermann, University of Tübingen, Germany.
:::
:::info This paper is available on arxiv under CC BY 4.0 license.
:::
:::info Lead image by ThisIsEngineering on Pexels.
:::
\
This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Abstraction: Computer Science Discourse | Sciencx (2025-07-06T23:58:11+00:00) How Let Bindings Improve Code Readability in Functional Programming. Retrieved from https://www.scien.cx/2025/07/06/how-let-bindings-improve-code-readability-in-functional-programming/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
