This content originally appeared on HackerNoon and was authored by Cosmological thinking: time, space and universal causation
Table of Links
2 Muons vs. Protons
3 Muon Colliders Are Gauge Boson Colliders
3.1 From the effective vector approximation to PDFs
3.2 PDFs with broken electroweak symmetry
4 Physics
4.1 Electroweak symmetry breaking
5 Complementarity
6 Summary and Future Directions
3.1 From the effective vector approximation to PDFs
The soft and collinear divergences inherent to theories of charged particles coupled to gauge bosons yield physical logarithmic enhancements that can spoil the convergence of perturbation theory. When considering colliding beams of charged particles, it is important to acknowledge our inherent inability to experimentally distinguish a single state in isolation from one that has emitted a nearly collinear or very soft additional particle. A framework for addressing this problem was first written down in 1934 by Weizsaecker [55] and Williams [56]; this is what is known as the “effective photon approximation” or more generally the “effective vector approximation” (EVA):
\
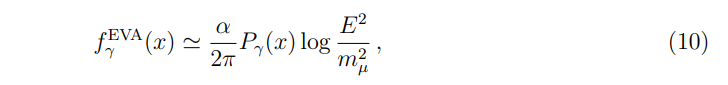
\ where the log is the result of soft emissions, and the QED splitting function
\
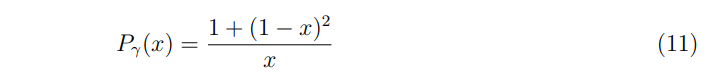
\ can be derived by taking the collinear limit of a tree-level 1 → 2 process computed using perturbative QED. Note that in this approximation, E is the beam energy of the colliding charged particle while the emitted photon energy is given by Q = xE, where x is the momentum fraction carried by the photon.
\

\ where the splitting function Pγ(x) is still given by Eq. (11), and we are taking the gauge coupling to be fixed for simplicity. This is of course the logarithmic behavior one would find when computing at fixed order in perturbation theory, and additionally it follows from solving the DGLAP evolution equations for QED given in Eq. (15) to leading log order, as it must for self consistency. As we will see in what follows, simply solving for the leading log approximation given in Eq. (12) for the full system of partons relevant at a muon collider provides a good approximation to the full solution to the DGLAP equations. Note that since it is trivial to implement, we do allow the gauge coupling to run (at one-loop order) when computing the leading log PDFs that are used to make some of the cross-section predictions below.
\
:::info Authors:
(1) Hind Al Ali, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(2) Nima Arkani-Hamed, School of Natural Sciences, Institute for Advanced Study, Princeton, NJ, 08540, USA;
(3) Ian Banta, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(4) Sean Benevedes, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(5) Dario Buttazzo, INFN, Sezione di Pisa, Largo Bruno Pontecorvo 3, I-56127 Pisa, Italy;
(6) Tianji Cai, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(7) Junyi Cheng, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(8) Timothy Cohen, Institute for Fundamental Science, University of Oregon, Eugene, OR 97403, USA;
(9) Nathaniel Craig, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(10) Majid Ekhterachian, Maryland Center for Fundamental Physics, University of Maryland, College Park, MD 20742, USA;
(11) JiJi Fan, Department of Physics, Brown University, Providence, RI 02912, USA;
(12) Matthew Forslund, C. N. Yang Institute for Theoretical Physics, Stony Brook University, Stony Brook, NY 11794, USA;
(13) Isabel Garcia Garcia, Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA;
(14) Samuel Homiller, Department of Physics, Harvard University, Cambridge, MA 02138, USA;
(15) Seth Koren, Department of Physics and Enrico Fermi Institute, University of Chicago, Chicago, IL 60637, USA;
(16) Giacomo Koszegi, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(17) Zhen Liu, Maryland Center for Fundamental Physics, University of Maryland, College Park, MD 20742, USA and School of Physics and Astronomy, University of Minnesota, Minneapolis, MN 55455, USA;
(18) Qianshu Lu, Department of Physics, Harvard University, Cambridge, MA 02138, USA;
(19) Kun-Feng Lyu, Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong S.A.R., P.R.C;
(20) Alberto Mariotti, Theoretische Natuurkunde and IIHE/ELEM, Vrije Universiteit Brussel, and International Solvay Institutes, Pleinlaan 2, B-1050 Brussels, Belgium;
(21) Amara McCune, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(22) Patrick Meade, C. N. Yang Institute for Theoretical Physics, Stony Brook University, Stony Brook, NY 11794, USA;
(23) Isobel Ojalvo, Princeton University, Princeton, NJ 08540, USA;
(24) Umut Oktem, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(25) Diego Redigolo, CERN, Theoretical Physics Department, Geneva, Switzerland and INFN Sezione di Firenze, Via G. Sansone 1, I-50019 Sesto Fiorentino, Italy;
(26) Matthew Reece, Department of Physics, Harvard University, Cambridge, MA 02138, USA;
(27) Filippo Sala, LPTHE, CNRS & Sorbonne Universite, 4 Place Jussieu, F-75252 Paris, France
(28) Raman Sundrum, Maryland Center for Fundamental Physics, University of Maryland, College Park, MD 20742, USA;
(29) Dave Sutherland, INFN Sezione di Trieste, via Bonomea 265, 34136 Trieste, Italy;
(30) Andrea Tesi, INFN Sezione di Firenze, Via G. Sansone 1, I-50019 Sesto Fiorentino, Italy and Department of Physics and Astronomy, University of Florence, Italy;
(31) Timothy Trott, Department of Physics, University of California, Santa Barbara, CA 93106, USA;
(32) Chris Tully, Princeton University, Princeton, NJ 08540, USA;
(33) Lian-Tao Wang, Department of Physics and Enrico Fermi Institute, University of Chicago, Chicago, IL 60637, USA;
(34) Menghang Wang, Department of Physics, University of California, Santa Barbara, CA 93106, USA.
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by Cosmological thinking: time, space and universal causation
Cosmological thinking: time, space and universal causation | Sciencx (2025-07-15T00:15:51+00:00) From Effective Vector Approximation to Muon PDFs: Unpacking Initial State Physics. Retrieved from https://www.scien.cx/2025/07/15/from-effective-vector-approximation-to-muon-pdfs-unpacking-initial-state-physics/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
