This content originally appeared on HackerNoon and was authored by Probabilistic
Table of Links
4 Empirical Evaluation
In this section, we present the results of the empirical evaluation for LIFAGU. To evaluate the performance of LIFAGU, we start with a non-parameterised FG G where all factors are known, serving as our ground truth. Afterwards, we remove the potential mappings for five to ten percent of the factors in G, yielding an incomplete FG G′ on which LIFAGU is run to obtain a PFG GLIFAGU. Each factor f ′ whose potentials are removed is chosen randomly under the constraint
\
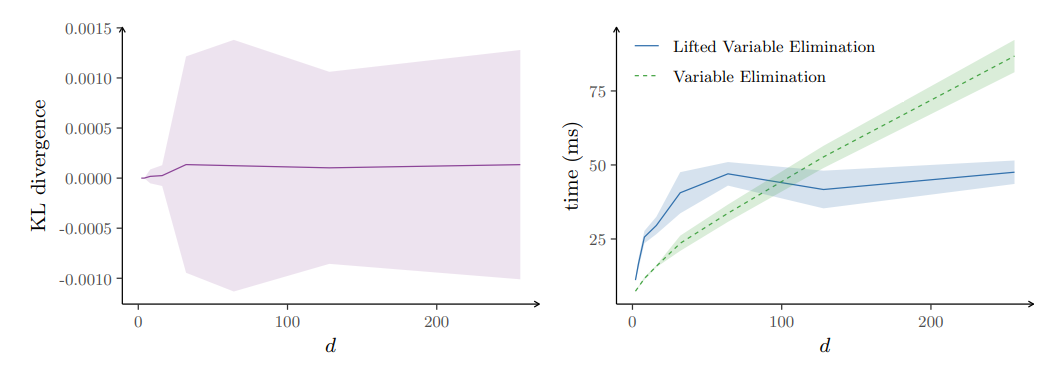
\ that there exists at least one other factor with known potentials that is possibly identical to f ′ . This constraint corresponds to the assumption that there exists at least one group to which a new individual can be added and it ensures that after running LIFAGU, probabilistic inference can be performed for evaluation purposes. Clearly, in our evaluation setting, there is not only a single new individual but instead a set of new individuals, given by the set of factors whose potentials are missing. We use a parameter d = 2, 4, 8, 16, 32, 64, 128, 256 to control the size of the FG G (and thus, the size of G′ ). More precisely, for each choice of d, we evaluate multiple input FGs which contain between 2d and 3d randvars (and factors, respectively). The potentials of the factors are randomly generated such that the ground truth G contains between three and five (randomly chosen) cohorts of randvars which should be grouped together, with one cohort containing roughly 50 percent of all randvars in G while the other cohorts share the remaining 50 percent of the randvars from G uniformly at random.
\ We set θ = 0 to ensure that each unknown factor is grouped with at least one known factor to be able to perform lifted probabilistic inference on GLIFAGU for evaluation. To assess the error made by LIFAGU for each choice of d, we pose d different queries to the ground truth G and to GLIFAGU, respectively. For each query, we compute the Kullback-Leibler (KL) divergence [10] between the resulting probability distributions for the ground truth G and GLIFAGU to measure the similarity of the query results. The KL divergence measures the difference of two distributions and its value is zero if the distributions are identical.
\ In the left plot of Fig. 4, we report the mean KL divergence over all queries for each choice of d. The ribbon around the line illustrates the standard deviation of the measured KL divergences. We find that the mean KL divergence is close to zero for all choices of d in practice. Both the mean KL divergence and the standard deviation of the KL divergences do not show any significant differences between the various values for d. Note that the depicted standard deviation is also very small for all choices of d due to the granularity of the y-axis. The maximum KL divergence measured for any choice of d is about 0.01.
\ Given our assumptions, a new individual actually belongs to a cohort and most cohorts behave not completely different. So normally, we trade off accuracy of query results for the ability to perform inference, which otherwise would not be possible at all. If the semantics cannot be fixed, missing potentials need to be guessed to be able to perform inference at all, probably resulting in worse errors. As we basically perform unsupervised clustering, errors might happen when grouping unknown factors with known factors. The error might be further reduced by increasing the effort when searching for known factors that are possible candidates for grouping with an unknown factor. For example, it is conceivable to increase the size of the neighbourhood during the search for possible identical factors at the expense of a higher run time expenditure.
\ In addition to the error measured by the KL divergence, we also report the run times of variable elimination on G and lifted variable elimination on the PFG computed by LIFAGU, i.e., GLIFAGU. The run times are shown in the right plot of Fig. 4. As expected, lifted variable elimination is faster than variable elimination for larger graphs and the run time of lifted variable elimination increases more slowly with increasing graph sizes than the run time of variable elimination. Hence, LIFAGU not only allows to perform probabilistic inference at all, but also speeds up inference by allowing for lifting probabilistic inference. Note that there are on average 24 different groups over all settings with the largest domain size being 87 (for the setting of d = 256), i.e., there are a lot of small groups (of size one) which diminish the advantage of lifted variable elimination over variable elimination. We could also obtain more compact PFGs by merging groups that are not fully identical but similar to a given extent such that the resulting PFG contains less different groups at the cost of a lower accuracy of query results. Obtaining a more compact PFG would most likely result in a higher speedup of lifted variable elimination compared to variable elimination.
\
5 Conclusion
In this paper, we introduce the LIFAGU algorithm to construct a lifted representation for an FG that possibly contains unknown factors. LIFAGU is a generalisation of the widespread CP algorithm and allows to transfer potentials from known factors to unknown factors by identifying symmetric subgraphs. Under the assumption that for every unknown factor there exists at least one known factor having a symmetric surrounding graph structure to it, LIFAGU is able to replace all unknown potentials in an FG by known potentials.
\
Acknowledgements
This work was partially supported by the BMBF project AnoMed. The research of Malte Luttermann was also partially supported by the Medical Cause and Effects Analysis (MCEA) project. This preprint has not undergone peer review or any post-submission improvements or corrections. The Version of Record of this contribution is published in Lecture Notes in Computer Science, Volume 14294, and is available online at https://doi.org/10.1007/978-3-031-45608-4 25.
\
References
Ahmadi, B., Kersting, K., Mladenov, M., Natarajan, S.: Exploiting Symmetries for Scaling Loopy Belief Propagation and Relational Training. Machine Learning 92, 91–132 (2013)
\
Braun, T., Moller, R.: Lifted Junction Tree Algorithm. In: Proceedings of KI 2016: Advances in Artificial Intelligence (KI-16). pp. 30–42. Springer (2016)
\
De Salvo Braz, R., Amir, E., Roth, D.: Lifted First-Order Probabilistic Inference. In: Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence (IJCAI-05). pp. 1319–1325. Morgan Kaufmann Publishers Inc. (2005)
\
De Salvo Braz, R., Amir, E., Roth, D.: MPE and Partial Inversion in Lifted Probabilistic Variable Elimination. In: Proceedings of the Twenty-First National Conference on Artificial Intelligence (AAAI-06). pp. 1123–1130. AAAI Press (2006)
\
Gehrke, M., M¨oller, R., Braun, T.: Taming Reasoning in Temporal Probabilistic Relational Models. In: Proceedings of the Twenty-Fourth European Conference on Artificial Intelligence (ECAI-20). pp. 2592–2599. IOS Press (2020)
\
Hoffmann, M., Braun, T., M¨oller: Lifted Division for Lifted Hugin Belief Propagation. In: Proceedings of the Twenty-Fifth International Conference on Artificial Intelligence and Statistics (AISTATS-22). pp. 6501–6510. PMLR (2022)
\
Kersting, K., Ahmadi, B., Natarajan, S.: Counting Belief Propagation. In: Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence (UAI-09). pp. 277–284. AUAI Press (2009)
\
Kisy´nski, J., Poole, D.: Constraint Processing in Lifted Probabilistic Inference. In: Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence (UAI-09). pp. 293–302. AUAI Press (2009)
\
Kschischang, F.R., Frey, B.J., Loeliger, H.A.: Factor Graphs and the Sum-Product Algorithm. IEEE Transactions on Information Theory 47, 498–519 (2001)
\
Kullback, S., Leibler, R.A.: On Information and Sufficiency. The Annals of Mathematical Statistics 22, 79–86 (1951)
\
Milch, B., Zettlemoyer, L.S., Kersting, K., Haimes, M., Kaelbling, L.P.: Lifted Probabilistic Inference with Counting Formulas. In: Proceedings of the TwentyThird AAAI Conference on Artificial Intelligence (AAAI-08). pp. 1062–1068. AAAI Press (2008)
\
Niepert, M., Van den Broeck, G.: Tractability through Exchangeability: A New Perspective on Efficient Probabilistic Inference. In: Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence (AAAI-14). pp. 2467–2475. AAAI Press (2014)
\
Poole, D.: First-Order Probabilistic Inference. In: Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence (IJCAI-03). pp. 985–991. Morgan Kaufmann Publishers Inc. (2003)
\
Taghipour, N., Fierens, D., Davis, J., Blockeel, H.: Lifted Variable Elimination: Decoupling the Operators from the Constraint Language. Journal of Artificial Intelligence Research 47, 393–439 (2013)
\
Weisfeiler, B., Leman, A.A.: The Reduction of a Graph to Canonical Form and the Algebra which Appears Therein. NTI, Series 2, 12–16 (1968), English translation by Grigory Ryabov available at https://www.iti.zcu.cz/wl2018/pdf/ wl paper translation.pdf
\
:::info Authors:
(1) Malte Luttermann[0009 −0005 −8591 −6839], Institute of Information Systems, University of Lubeck, Germany and German Research Center for Artificial Intelligence (DFKI), Lubeck, Germany (luttermann@ifis.uni-luebeck.de);
(2) Ralf Moller[0000 −0002 −1174 −3323], Institute of Information Systems, University of Lubeck, Germany and German Research Center for Artificial Intelligence (DFKI), Lubeck, Germany (moeller@ifis.uni-luebeck.de);
(3) Marcel Gehrke[0000 −0001 −9056 −7673], Institute of Information Systems, University of Lubeck, Germany (gehrke@ifis.uni-luebeck.de).
:::
:::info This paper is available on arxiv under ATTRIBUTION-SHAREALIKE 4.0 INTERNATIONAL license.
:::
\
This content originally appeared on HackerNoon and was authored by Probabilistic
Probabilistic | Sciencx (2025-08-26T12:15:02+00:00) When Graphs Have Gaps: LIFAGU Finds Symmetry and Speeds Up Inference. Retrieved from https://www.scien.cx/2025/08/26/when-graphs-have-gaps-lifagu-finds-symmetry-and-speeds-up-inference/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
