This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Table of Links
Translating To Sequent Calculus
Evaluation Within a Context
Insights
5.1 Evaluation Contexts are First Class
5.3 Let-Bindings are Dual to Control Operators
5.4 The Case-of-Case Transformation
5.5 Direct and Indirect Consumers
Conclusion, Data Availability Statement, and Acknowledgments
A. The Relationship to the Sequent Calculus
C. Operational Semantics of label/goto
4.2 Typing Rules for Core
The complete typing rules for Core are given in Figure 2, but we will present them step by step. We now have producers, consumers and statements as different syntactic categories. For each of these categories, we use a separate judgment form:
\

\ All typing judgments are also implicitly indexed by the program 𝑃 containing the top-level definitions. However, as these definitions are only needed when typechecking their calls (rule Call), we usually omit the index from the presentation.
\

\

\

\ 4.2.1 Data and Codata Types. Figure 2 contains the typing rules for both Pair and List; since their rules are so similar we only discuss those of Pair explicitly:
\
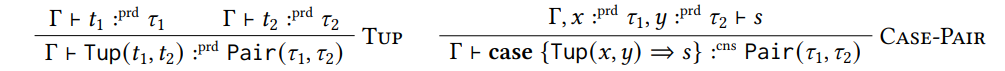
\ In the rule Tup we type a pair constructor Tup applied to two arguments as a producer, and in the rule Case-Pair we type the case, which pattern-matches on this constructor and brings two variables into scope, as a consumer.
\ The typing rules for codata types look exactly the same, only the roles of producers and consumers are swapped.
\
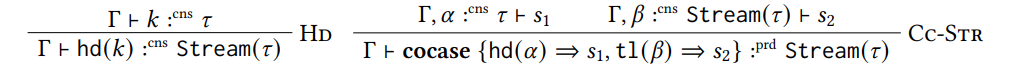
\ Most of the other rules directly correspond to a similar rule for Fun. When typing arithmetic expressions, for example, we only have to make sure all subterms have type Int.
\ We typecheck programs using the two rules Wf-Empty and Wf-Cons. The former is used to typecheck an empty program, and the rule Wf-Cons extends a typechecked program with a new top-level definition. When we typecheck the body of this top-level definition that we are about to add, we extend the program with this definition so that it can refer to itself recursively.
4.3 Type Soundness
In this section, we discuss the soundness of the type systems for both Fun and Core and show that the translation [−] preserves the typeability of terms. We follow Wright and Felleisen [1994] in presenting type soundness as the combination of a progress and a preservation theorem. Theorem 4.1 (Progress, Fun).
\ Theorem 4.1 (Progress, Fun). Let 𝑡 be a closed term in Fun, such that ⊢ 𝑡 : 𝜏 for some type 𝜏. Then either 𝑡 is a value or there is some term 𝑡 ′ such that 𝑡 ⊲ 𝑡 ′ .
\ This can easily be proved with an induction on typing derivations. Due to the presence of the label/goto construct, the standard formulation of the (strong) preservation theorem does not immediately hold for Fun (also see the discussion in Appendix C). The following weak form of preservation can again be easily proved by induction.
\ Theorem 4.2 ((Weak) Preservation, Fun). Let 𝑡, 𝑡′ be terms in Fun such that 𝑡 ⊲ 𝑡 ′ , Γ an environment and 𝑃 a program such that Γ ⊢𝑃 𝑡 : 𝜏. Then there is a type 𝜏 ′ such that Γ ⊢𝑃 𝑡 ′ : 𝜏 ′ .
\ The usual strong preservation theorem requires 𝜏 ′ = 𝜏. But in fact, a slight variation of this strong form can be proved for Fun by adapting the technique found in Section 6 in [Wright and Felleisen 1994]. Thus, strong type soundness still does hold.
\ Before we can state the analogous theorems for Core, we will need an additional definition as a termination condition for evaluation.
\ Definition 4.3 (Terminal statement). If 𝔭 is a producer value in Core and ⋆ a covariable which does not appear free in 𝔭, then ⟨𝔭 | ⋆⟩ is called a terminal statement.
\ Terminal statements in Core have the same role as values in Fun. Some sequent-calculus-based languages use a special statement Done instead of terminal statements for this purpose.
\ Theorem 4.4 (Progress, Core). Let 𝑠 be a focused statement in Core such that ⊢ 𝑠. Then either 𝑠 is a terminal statement, or there is some 𝑠 ′ such that 𝑠 ⊲ 𝑠 ′ .
\ For this theorem, we require 𝑠 to be focused, in contrast to Fun, where progress holds for any (well-typed) term. This is because we have used static focusing for full evaluation in Core. If we used dynamic focusing instead, this requirement could be dropped, corresponding to using evaluation contexts (dynamic) in Fun, instead of a translation to normal form (static).
\ The Preservation theorem for Core is analogous to Fun.
\ Theorem 4.5 (Preservation, Core). Let 𝑠, 𝑠′ be statements in Core with 𝑠 ⊲ 𝑠 ′ , Γ an environment and 𝑃 a program. If Γ ⊢𝑃 𝑠, then Γ ⊢𝑃 𝑠 ′ .
\
\

\ \ Lastly, we come to an important property of the translation between these languages:
\
\

\ \
:::info Authors:
(1) David Binder, University of Tübingen, Germany;
(2) Marco Tzschentke, University of Tübingen, Germany;
(3) Marius Muller, University of Tübingen, Germany;
(4) Klaus Ostermann, University of Tübingen, Germany.
:::
:::info This paper is available on arxiv under CC BY 4.0 license.
:::
\
This content originally appeared on HackerNoon and was authored by Abstraction: Computer Science Discourse
Abstraction: Computer Science Discourse | Sciencx (2025-07-08T08:00:03+00:00) How Typing Rules and Type Soundness Work in Core and Fun Programming Languages. Retrieved from https://www.scien.cx/2025/07/08/how-typing-rules-and-type-soundness-work-in-core-and-fun-programming-languages/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
